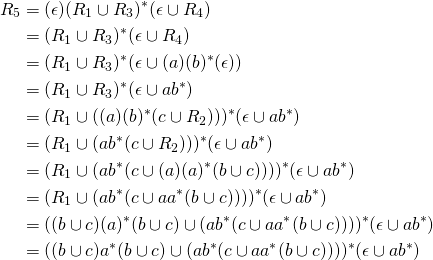The GNFA method is a procedure to convert any given NFA to an equivalent regular expression. The idea is to rip out one state at a time, while modifying the transitions to reflect the changes. Here is an example explaining the process in detail
NFA
Consider the following NFA
| State | |||
|---|---|---|---|
This can be expressed as the following state transition diagram
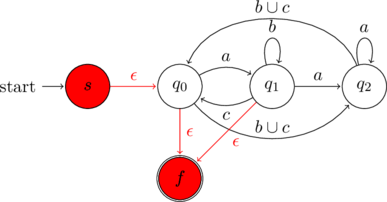
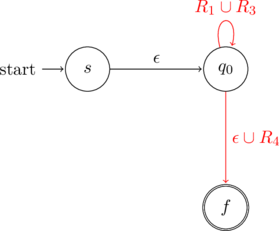
Adding start and final states
The first step is to add a new start and a single new final state. The new start state is labeled as ![]() . The new start state has an
. The new start state has an ![]() transition to the original start state of the NFA. The new final state is labeled as
transition to the original start state of the NFA. The new final state is labeled as ![]() . All the final state(s) in the original NFA have an
. All the final state(s) in the original NFA have an ![]() transition to the new final state. The two new additions are marked in color.
transition to the new final state. The two new additions are marked in color.
Every state except ![]() and
and ![]() needs to ripped out. The order of choosing a state to rip out doesn’t really matter.
needs to ripped out. The order of choosing a state to rip out doesn’t really matter.
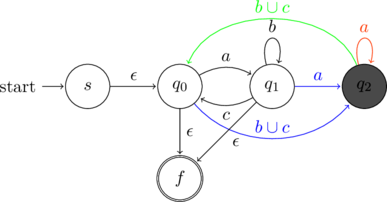
Rip 
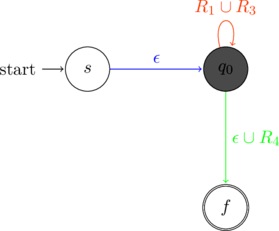
Consider the state ![]() . The incoming (blue), looping (orange) and outgoing (green) transitions for this state are marked in different colors.
. The incoming (blue), looping (orange) and outgoing (green) transitions for this state are marked in different colors.
Thus, there are two paths through ![]() . This is summarized below
. This is summarized below
| Path | Incoming | Loop | Outgoing |
|---|---|---|---|
To rip state ![]() , the transitions along these paths need to accounted for. The equivalent transition is defined as
, the transitions along these paths need to accounted for. The equivalent transition is defined as
Applying this to the table above
| Path | Incoming | Loop | Outgoing | Equivalent Transition |
|---|---|---|---|---|
After ripping the state ![]() the NFA changes to the following
the NFA changes to the following
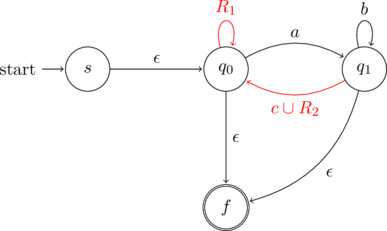
Rip 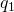
Consider the state ![]() . The incoming (blue), looping (orange) and outgoing (green) transitions for this state are marked in different colors.
. The incoming (blue), looping (orange) and outgoing (green) transitions for this state are marked in different colors.
Thus, there are two paths through ![]() . This is summarized below
. This is summarized below
| Path | Incoming | Loop | Outgoing |
|---|---|---|---|
To rip state ![]() , the transitions along these paths need to accounted for. The equivalent transition is defined as
, the transitions along these paths need to accounted for. The equivalent transition is defined as
Applying this to the table above
| Path | Incoming | Loop | Outgoing | Equivalent Transition |
|---|---|---|---|---|
After ripping the state ![]() the NFA changes to the following
the NFA changes to the following
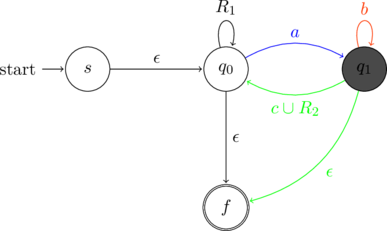
Rip 
Consider the state ![]() . The incoming (blue), looping (orange) and outgoing (green) transitions for this state are marked in different colors.
. The incoming (blue), looping (orange) and outgoing (green) transitions for this state are marked in different colors.
Thus, there is one path through ![]() . This is summarized below
. This is summarized below
| Path | Incoming | Loop | Outgoing |
|---|---|---|---|
To rip state ![]() , the transitions along these paths need to accounted for. The equivalent transition is defined as
, the transitions along these paths need to accounted for. The equivalent transition is defined as
Applying this to the table above
| Path | Incoming | Loop | Outgoing | Equivalent Transition |
|---|---|---|---|---|
After ripping the state ![]() the NFA changes to the following
the NFA changes to the following
Regular Expression
The equivalent regular expression is the transition from ![]() to
to ![]() .
.
Depending on the order of ripping out states, the NFA may be converted to different equivalent regular expressions.