A language is decidable if there is a Turing Machine that halts and accepts strings that belong to the language, and halts and rejects strings that do not belong to the language.
ADFA
There exists a TM that decides the above language. Given the string encoding of a DFA ![]() and some string
and some string ![]() , a TM can decide whether
, a TM can decide whether ![]() accepts
accepts ![]() .
.
High-Level Description
On input ![]()
- Check whether
 indeed encodes a DFA. If not, reject.
indeed encodes a DFA. If not, reject. - Record that
 is in the start state
is in the start state  , reading first symbol of
, reading first symbol of 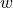 .
. - Based on the current state of
 and current symbol of
and current symbol of 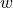 , compute the new state. Change the current state to the new state and to the next symbol of
, compute the new state. Change the current state to the new state and to the next symbol of 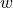 . Repeat this step until all of
. Repeat this step until all of 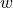 is read.
is read. - If
 is in a final state, accept. Else reject.
is in a final state, accept. Else reject.
Steps 2 and 3 can be summarized as simulating the DFA ![]() on the input
on the input ![]() . Since all these steps take a finite amount of time, it is guaranteed that the machine halts and decides.
. Since all these steps take a finite amount of time, it is guaranteed that the machine halts and decides.
ANFA
High-Level Description
On input ![]()
- Check whether
 indeed encodes a NFA. If not, reject.
indeed encodes a NFA. If not, reject. - Convert the NFA
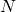 to an equivalent DFA
to an equivalent DFA  using the power-set method.
using the power-set method. - Run
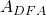 on
on 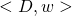 .
.
Thus, ![]() is decidable because it can be reduced to
is decidable because it can be reduced to ![]() .
.
AREX
High-Level Description
On input ![]()
- Check whether
 indeed encodes a regular expression. If not, reject.
indeed encodes a regular expression. If not, reject. - Convert the regular expression
 to an equivalent NFA
to an equivalent NFA  using the GNFA method.
using the GNFA method. - Run
 on
on 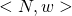 .
.
Thus, ![]() is decidable because it can be reduced to
is decidable because it can be reduced to ![]() .
.
ARG
High-Level Description
On input ![]()
- Check whether
 indeed encodes a regular grammar. If not, reject.
indeed encodes a regular grammar. If not, reject. - Convert the regular grammar
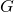 to an equivalent NFA
to an equivalent NFA 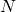 .
. - Run
 on
on 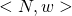 .
.
Thus, ![]() is decidable because it can be reduced to
is decidable because it can be reduced to ![]() .
.