Consider the problem of building a Nondeterministic Finite Automaton (NFA) over to accept ternary numbers that are a multiple of but not a multiple of . Here are the first ternary numbers.

Ternary	Decimal
	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10
	11
	12
	13
	14
	15
	16
	17
	18

Multiples of 3

From the above table, the ternary numbers that are a multiple of always end with a . Notice that, is indeed a multiple of .

Multiples of 9

From the above table, the ternary numbers that are a multiple of always end with a . Notice that, is indeed a multiple of .

Multiples of 3 but not a Multiple of 9

Extrapolating from the previous two observations, the ternary numbers that are a multiple of but not a multiple of are numbers that end with a single . Thus, the last two digits can be either or . The digits before these two digits do not matter.

Regex

A regular expression to express this would be

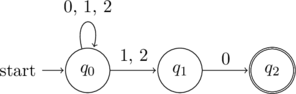
NFA

The above regular expression can expressed as the following NFA