Consider the problem of building a Deterministic Finite Automaton (DFA) over ![]() to accept ternary numbers that are multiples of 5. For the sake of simplicity, assume that the empty string,
to accept ternary numbers that are multiples of 5. For the sake of simplicity, assume that the empty string, ![]() , should be accepted.
, should be accepted.
States
The resulting DFA will have ![]() states. Each state will keep track of one of five possible remainders –
states. Each state will keep track of one of five possible remainders – ![]() .
.
For example, the state ![]() , keeps track of the information that the ternary string read upto this point, when divided by
, keeps track of the information that the ternary string read upto this point, when divided by ![]() , leaves remainder
, leaves remainder ![]() .
.
Tracking remainder
Consider the ternary string ![]() . The decimal equivalent of this ternary number is
. The decimal equivalent of this ternary number is ![]() .
. ![]() when divided by
when divided by ![]() , leaves remainder
, leaves remainder ![]() . Thus, if the above DFA already read the input
. Thus, if the above DFA already read the input ![]() , it will currently be in state
, it will currently be in state ![]() .
.
Symbol 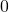
If the string ![]() is followed by a
is followed by a ![]() , the ternary number
, the ternary number ![]() is equivalent to
is equivalent to ![]() in decimal. In effect, seeing a single
in decimal. In effect, seeing a single ![]() at the end of a ternary string, multiplies the integer equivalent by
at the end of a ternary string, multiplies the integer equivalent by ![]() . The same logic applies to the remainder.
. The same logic applies to the remainder. ![]() when divided by
when divided by ![]() , leaves remainder
, leaves remainder ![]() , which is the same as
, which is the same as ![]() .
.
| Old Ternary | Old Decimal | Symbol | New Ternary | New Decimal | ||
Symbol 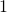
If the string ![]() is followed by a
is followed by a ![]() , the ternary number
, the ternary number ![]() is equivalent to
is equivalent to ![]() in decimal. In effect, seeing a single
in decimal. In effect, seeing a single ![]() at the end of a ternary string, multiplies the integer equivalent by
at the end of a ternary string, multiplies the integer equivalent by ![]() and then adds a
and then adds a ![]() . The same logic applies to the remainder.
. The same logic applies to the remainder. ![]() when divided by
when divided by ![]() , leaves remainder
, leaves remainder ![]() , which is the same as
, which is the same as ![]() .
.
| Old Ternary | Old Decimal | Symbol | New Ternary | New Decimal | ||
Symbol 
If the string ![]() is followed by a
is followed by a ![]() , the ternary number
, the ternary number ![]() is equivalent to
is equivalent to ![]() in decimal. In effect, seeing a single
in decimal. In effect, seeing a single ![]() at the end of a ternary string, multiplies the integer equivalent by
at the end of a ternary string, multiplies the integer equivalent by ![]() and then adds a
and then adds a ![]() . The same logic applies to the remainder.
. The same logic applies to the remainder. ![]() when divided by
when divided by ![]() , leaves remainder
, leaves remainder ![]() , which is the same as
, which is the same as ![]() .
.
| Old Ternary | Old Decimal | Symbol | New Ternary | New Decimal | ||
General Formula
Consider any ternary string ![]() , that leaves remainder
, that leaves remainder ![]() when divided by
when divided by ![]() . Upon seeing a new symbol after
. Upon seeing a new symbol after ![]() , the remainder changes as follows
, the remainder changes as follows
| Ternary String | Remainder | New Symbol | New Remainder |
![]() can take values from
can take values from ![]() to
to ![]() . Substituting these values in the above table, generates the following
. Substituting these values in the above table, generates the following
| Remainder | New Symbol | New Remainder |
Transitions
In the above table, the first column maps to one of the states of the DFA. The second column, maps to a transition symbol. The third column maps to the state the transition points to. Converting the table to states and transitions results in
| From State | Symbol | To State |
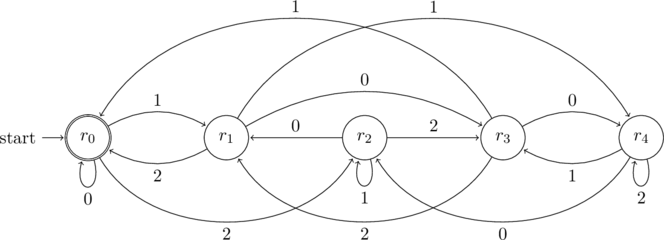
Since, the DFA has to accept strings that are multiples of ![]() , the state
, the state ![]() will be the only final state.
will be the only final state.
DFA
Combining the states and the transition table, the resulting DFA is shown below