Consider the following language
![]() is undecidable. This can be proved using contradiction.
is undecidable. This can be proved using contradiction.
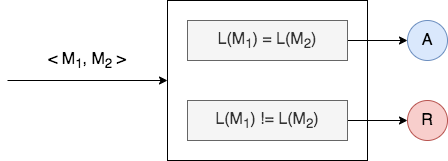
Suppose to the contrary that that there exists a TM, ![]() , that decides
, that decides ![]() . This machine takes
. This machine takes ![]() as an input. It accepts if
as an input. It accepts if ![]() and rejects otherwise.
and rejects otherwise.

Using ![]() , build another TM
, build another TM ![]() as follows
as follows
On input ![]()
- Construct a new TM
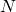 which rejects everything.
which rejects everything. - Run
 on
on  . If
. If  accepts, accept. If
accepts, accept. If  rejects, reject.
rejects, reject.
Notice the language of the TM ![]() is empty. If
is empty. If ![]() accepts
accepts ![]() , then the language of
, then the language of ![]() is also empty.
is also empty.
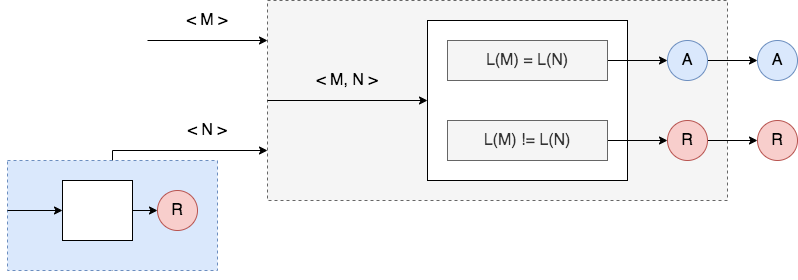
 . The shaded blue box is
. The shaded blue box is 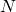 . The shaded grey box is
. The shaded grey box is  .
.The machine ![]() takes
takes ![]() as an input. It accepts if
as an input. It accepts if ![]() and rejects otherwise. In essence, this is a machine that decides
and rejects otherwise. In essence, this is a machine that decides ![]() . We say that
. We say that ![]() reduces to
reduces to ![]() .
.
If ![]() is decidable, this makes
is decidable, this makes ![]() decidable as well. This is a contradiction. Since
decidable as well. This is a contradiction. Since ![]() is undecidable,
is undecidable, ![]() is also undecidable.
is also undecidable.