Branch prediction is an optimization that tries to guess the outcome of a conditional operation instruction and prepare for the most likely result. A digital circuit that performs this operation is known as a branch predictor. A branch prediction must correctly guess

• Is the instruction a branch operation?
• Is it taken (condition = true)?
• If taken, what is the target PC?

Correct predictions do not affect the CPI. However, incorrect predictions introduce the cost of mispredicting.

Static Branch Prediction

A static mechanism does not rely on information about the dynamic history of the code being executed. Instead, it predicts the outcome of a branch based solely on the branch instruction.

Conditional jump always not taken

Always predict that a conditional jump will not be taken, so always fetch the next sequential instruction.

Backward branches taken, forward branches no taken

A backward branch is one that has a target address that is lower than its own address. This technique can help with prediction accuracy of loops, which are usually backward-pointing branches, and are taken more often than not taken.

Programmer direction

The programmer can also provide the predicted direction

if (likely(x)) { ... }
if (unlikely(error)) { ... }

Dynamic Branch Prediction

Dynamic branch prediction uses past information about taken or not taken branches gathered at run-time to predict the outcome of a branch.

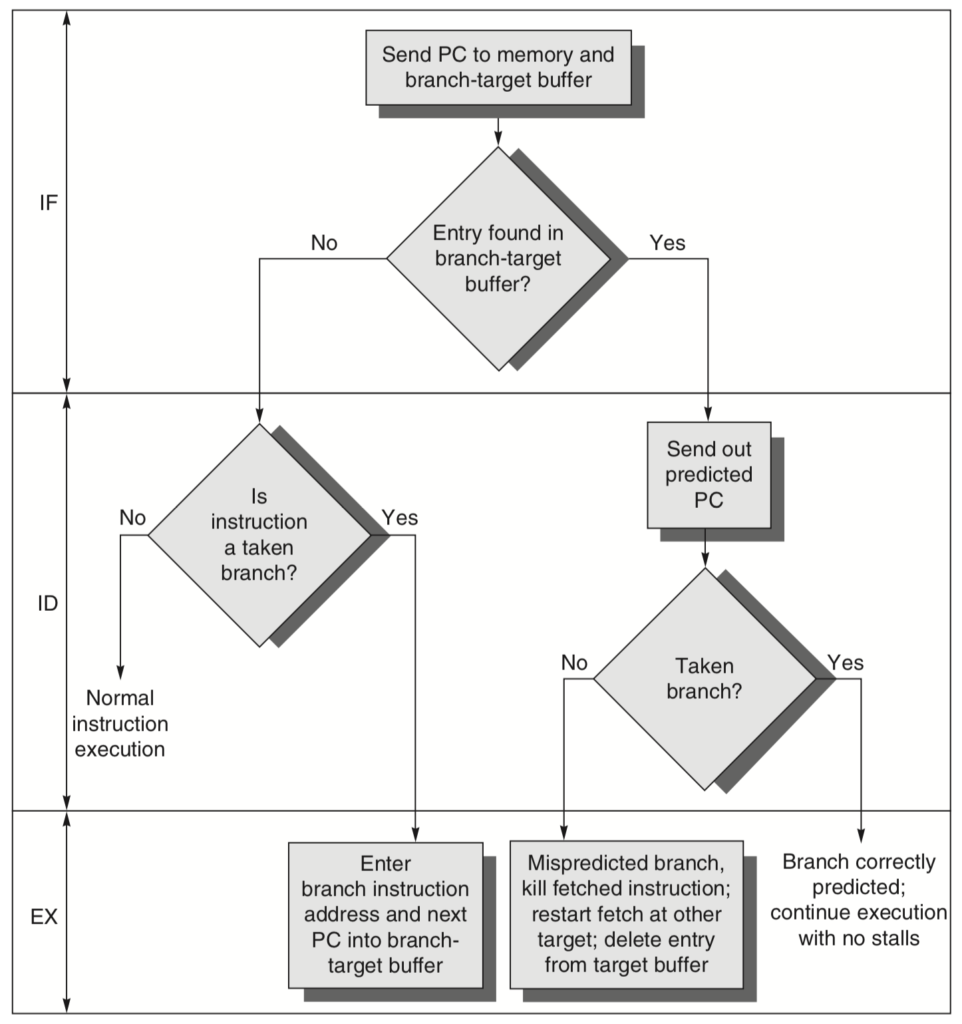
Branch Target Buffer (BTB)

A branch predictor tells us whether or not a branch is taken, but still requires the calculation of the branch target. A Branch Target Buffer is a structure that caches the destination PC or destination instruction for a branch. It is usually organized as a cache with tags. For lookup to be fast ( clock cycle) BTB should be small. It cannot have entry for all possible PCs. The least significant bits (stripped of the instruction size) of PC are used to index the BTB.

There is no branch penalty if everything is correctly predicted and the branch is found in the target buffer. If the branch is not correctly predicted, the penalty is equal to one clock cycle to update the buffer with the correct information (during which an instruction cannot be fetched) and one clock cycle, if needed, to restart fetching the next correct instruction for the branch. If the branch is not found and taken, a two-cycle penalty is encountered, during which time the buffer is updated.

Branch History Table (BHT)

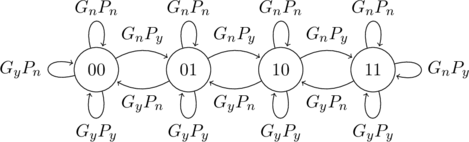
Branch History Table (BHT) is a small memory indexed by the lower portion of the address of the branch instruction. The memory contains a bit that says whether the branch was recently taken or not. If it is taken the branch address is read from BTB else PC is incremented by 1.
This simple -bit prediction has a performance shortcoming: even if a branch is almost always taken, we can predict incorrectly twice, rather than once, when it is not taken.

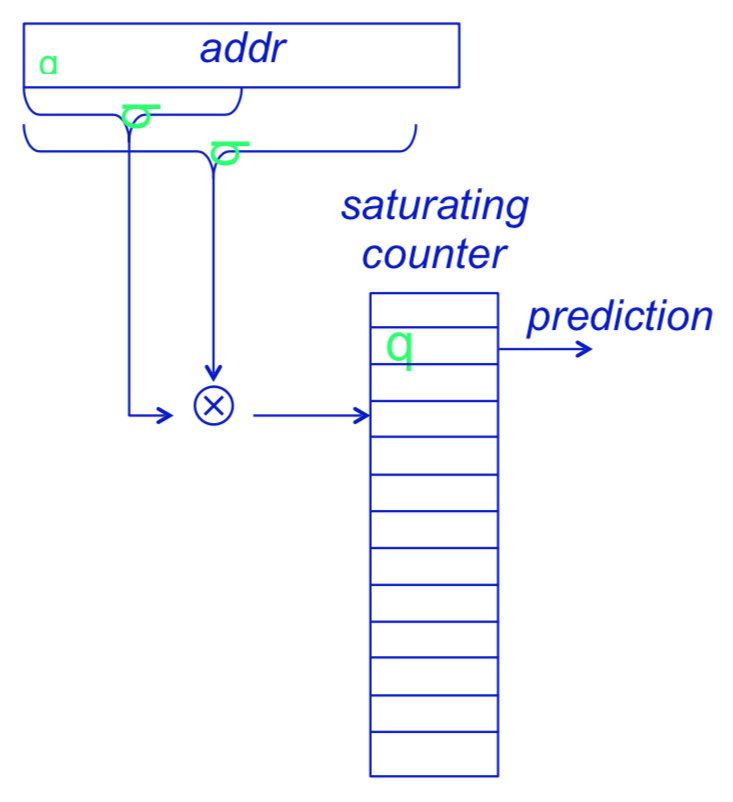
2-Bit Predictor

In a 2-bit scheme (2BP, 2BC), a prediction must be wrong twice before it is changed. The more significant bit of the predictor is the predictor bit. The less significant bit is the hysteresis/conviction bit. By using bits rather than , a branch that strongly favors taken or not taken—as many branches do—will be mispredicted only once. The bits are used to encode the four states in the system. The -bit scheme is actually a specialization of a more general scheme that has an n-bit saturating counter for each entry in the prediction buffer. With an n-bit counter, the counter can take on values between and : When the counter is greater than or equal to one-half of its maximum value (), the branch is predicted as taken; otherwise, it is predicted as untaken.

Strong Not Taken. Weak Not Taken. Weak Taken. Strong Taken.

Correlating Branch Predictors

if (aa==2)
    aa=0;
if (bb==2)
    bb=0
if (aa!=bb)

In the above code, the behavior of branch \texttt{b3} is correlated with the behavior of branches \texttt{b1} and \texttt{b2}.

Branch predictors that use the behavior of other branches to make a prediction are called correlating predictors or two-level predictors. Existing correlating predictors add information about the behavior of the most recent branches to decide how to predict a given branch.

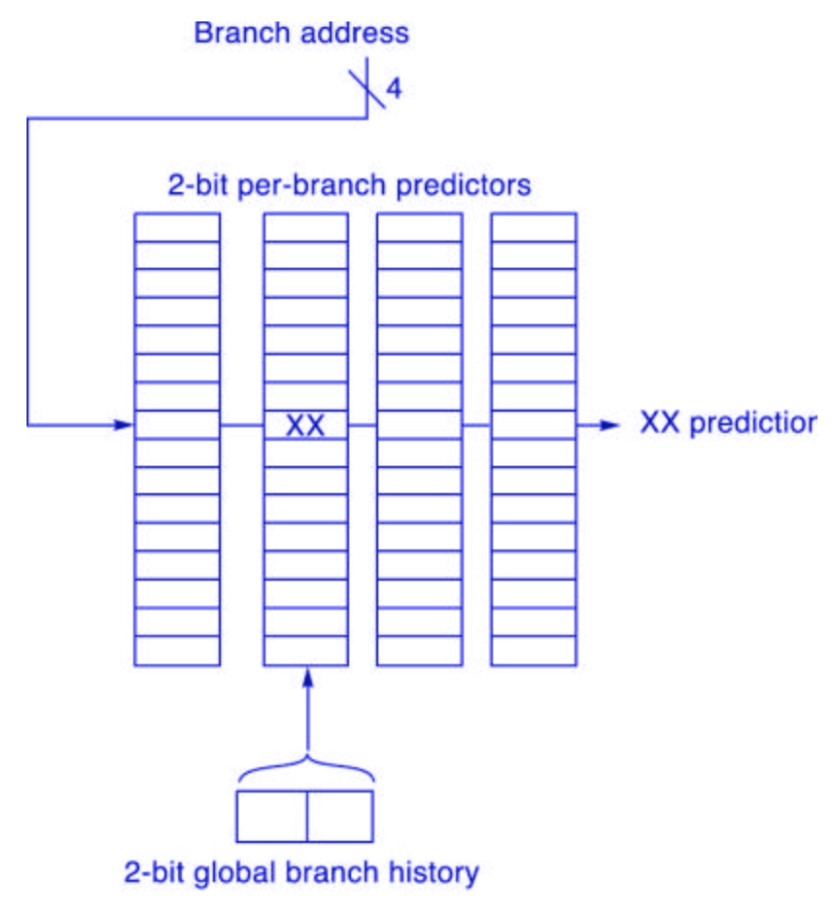
An predictor uses the behavior of the last branches to choose from branch predictors, each of which is an -bit predictor for a single branch.

The global history of the most recent branches can be recorded in an -bit shift register, where each bit records whether the branch was taken or not taken. The branch-prediction buffer can then be indexed using a concatenation of the low-order bits from the branch address with the -bit global history.

PShare

PShare stands for Private History Shared Counters. This keeps track of local information. Thus, these are good for isolated branch code. For example, checking for even or odd.

GShare

GShare stands for Global History Shared Counters. This keeps track of global information. Thus, these are good for correlated branch code.

Tournament Predictor

Tournament Predictor is a branch predictor with multiple predictions for each branch and a selection mechanism that chooses which predictor to enable for a given branch. A typical tournament predictor might contain two predictions for each branch index: one based on local information and one based on global branch behavior.

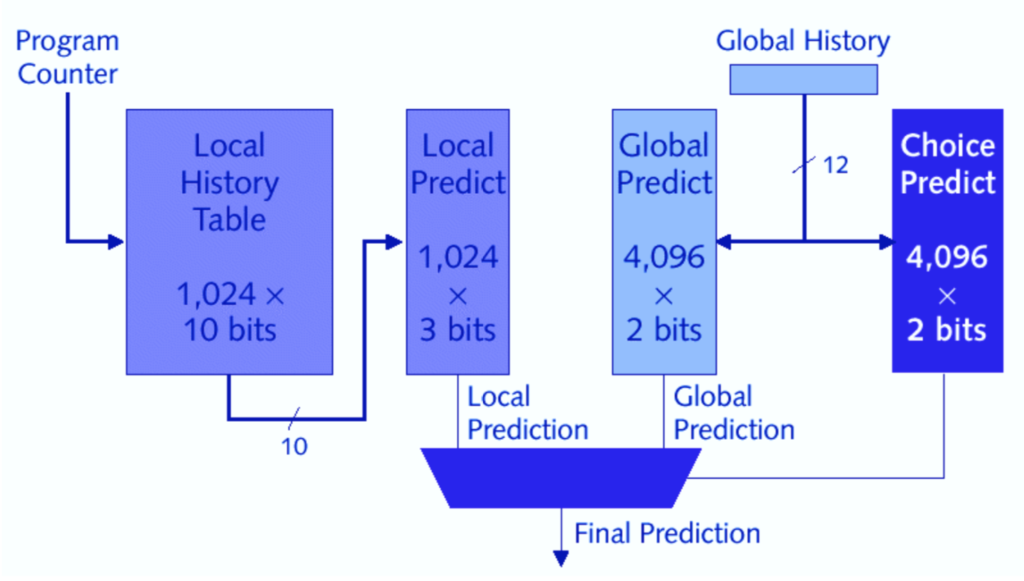
A selector (Meta-Predictor (array of 2BCs)) would choose which predictor to use for any given prediction. Both PShare and GShare predictors are trained on all branches. The Meta-Predictor favors whichever of the two predictors has been more accurate.

If both predictors are correct/wrong, the entry in Meta-Predictor is not changed. If PShare is correct but GShare is wrong, the entry is incremented. If GShare is wrong but PShare is corerct, the entry is decremented. A higher Meta-Predictor entry will chose PShare and a lower Meta-Predictor entry will chose GShare.

Return Address Stack (RAS)

A function return instruction is always taken. Since functions can be called from multiple locations a simple BTB cannot predict the target address. The RAS is a separate predictor to predict function returns. For every function call the address of the function is pushed to the top of the RAS. The function return target is predicted by popping from the top of the RAS.

When the RAS is full it is better to wrap around rather than stop pushing. The first RAS address will be main which is called only once. So it is better to overwrite these entries to provide room for functions deeper in the code that will be called multiple times.