Chomsky Normal Form - The Beard Sage

Definition

A Context-Free Grammar (CFG) is in Chomsky Normal Form (CNF) if every rule is of the form

$\begin{equation*} A \rightarrow BC \end{equation*}$

$\begin{equation*} A \rightarrow a \end{equation*}$

$\begin{equation*} S \rightarrow \epsilon \end{equation*}$

where $A \in V$ , $B, C \in V \setminus \{S\}$ , $a \in \Sigma$ and $S$ is the start variable. Note that the start variable cannot be present in the RHS of any rule.

CFG to a CFG in CNF

Consider the CFG to generate strings with balanced paranthesis

$\begin{equation*} S \rightarrow (S)S|[S]S|\epsilon \end{equation*}$

Every CFG can be converted to a CFG in CNF by following the steps below.

1. No start variable on RHS of a rule

This can be done by adding a new start variable $S'$ .

$\begin{align*} S' &\rightarrow S \\ S &\rightarrow (S)S|[S]S|\epsilon \\ \end{align*}$

2. Null Variables

a. Determine which variables are nullable

A variable is nullable if it can generate $\epsilon$ . The nullable variables for the above grammar are

$\begin{equa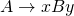tion*} S, S' \end{equation*}$

b. Whenever $A \rightarrow xBy$ and $B$ is nullable, add rule $A \rightarrow xy$

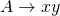
In essence, replace every instance of a nullable variable with $\epsilon$ and consider all possiblities.

$\begin{align*} S' &\rightarrow S|\epsilon \\ S &\rightarrow (S)S|()S|(S)|()|[S]S|[]S|[S]|[]|\epsilon \\ \end{align*}$

c. Remove all $\epsilon$ rules except for $S \rightarrow \epsilon$ (if present)

Now that all nullable variables generating $\epsilon$ is accounted for, these rules can be removed.

$\begin{align*} S' &\rightarrow S|\epsilon \\ S &\rightarrow (S)S|()S|(S)|()|[S]S|[]S|[S]|[] \\ \end{align*}$

3. Eliminate Unit Rules

Unit rules are of the type $A \rightarrow B$ where both $A$ and $B$ are variables. Replacing $B$ with $B$ ‘s RHS expansion will eliminate this unit rule.

$\begin{align*} S' &\rightarrow (S)S|()S|(S)|()|[S]S|[]S|[S]|[]|\epsilon \\ S &\rightarrow (S)S|()S|(S)|()|[S]S|[]S|[S]|[] \\ \end{align*}$

4. Ensure that every RHS of length at least $2$ contains only variables

This step involves creating new rules of the type $A \rightarrow a$ where $A$ is a variable and $a$ is a terminal. Define the following new rules

$\begin{align*} T_( &\rightarrow ( \\ T_) &\rightarrow ) \\ T_[ &\rightarrow [ \\ T_] &\rightarrow ] \\ \end{align*}$

The grammar is then modified to

$\begin{align*} S' &\rightarrow T_(ST_)S|T_(T_)S|T_(ST_)|T_(T_)|T_[ST_]S|T_[T_]S|T_[ST_]|T_[T_]|\epsilon \\ S &\rightarrow T_(ST_)S|T_(T_)S|T_(ST_)|T_(T_)|T_[ST_]S|T_[T_]S|T_[ST_]|T_[T_] \\ \end{align*}$

5. Breakup RHS of length greater than $2$

RHS of length greater than $2$ can broken down into sequential chunks of $2$ . For example $S \rightarrow T_(ST_)S$ can be written as

$\begin{align*} S &\rightarrow BS \\ B &\rightarrow AT_) \\ A &\rightarrow T_(S \\ \end{align*}$

The final grammar in CNF is as follows

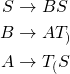
$\begin{align*} S' &\rightarrow BS|CS|AT_)|T_(T_)|ES|FS|DT_]|T_[T_]|\epsilon \\ S &\rightarrow BS|CS|AT_)|T_(T_)|ES|FS|DT_]|T_[T_] \\ A &\rightarrow T_(S \\ B &\rightarrow AT_) \\ C &\rightarrow T_(T_) \\ D &\rightarrow T_[S \\ E &\rightarrow DT_] \\ F &\rightarrow T_[T_] \\ T_( &\rightarrow ( \\ T_) &\rightarrow ) \\ T_[ &\rightarrow [ \\ T_] &\rightarrow ] \\ \end{align*}$

Definition

CFG to a CFG in CNF

1. No start variable on RHS of a rule

2. Null Variables

a. Determine which variables are nullable

b. Whenever and is nullable, add rule

c. Remove all rules except for (if present)

3. Eliminate Unit Rules

4. Ensure that every RHS of length at least contains only variables

5. Breakup RHS of length greater than

Leave a Reply Cancel reply

b. Whenever $A \rightarrow xBy$ and $B$ is nullable, add rule $A \rightarrow xy$

c. Remove all $\epsilon$ rules except for $S \rightarrow \epsilon$ (if present)

4. Ensure that every RHS of length at least $2$ contains only variables

5. Breakup RHS of length greater than $2$