Consider Context-Free Languages (CFLs) ![]() and
and ![]() , and assume that
, and assume that ![]() for some Context-Free Grammar (CFG)
for some Context-Free Grammar (CFG) ![]() and
and ![]() for some CFG
for some CFG ![]() . Note that both the CFGs share the same alphabet
. Note that both the CFGs share the same alphabet ![]() .
.
Context-Free Languages are closed under the following operations
Union
Consider the following grammar
Then ![]() , and therefore CFLs are closed under union. In essence, we are adding a new start variable
, and therefore CFLs are closed under union. In essence, we are adding a new start variable ![]() and the new start variable can go to either of
and the new start variable can go to either of ![]() or
or ![]() .
.
Concatenation
Consider the following grammar
Then ![]() , and therefore CFLs are closed under concatenation. In essence, we are adding a new start variable
, and therefore CFLs are closed under concatenation. In essence, we are adding a new start variable ![]() and the new start variable goes to
and the new start variable goes to ![]() .
.
Kleene Star
Consider the following grammar
Then ![]() , and therefore CFLs are closed under star. In essence, we are adding a new start variable and the new start variable
, and therefore CFLs are closed under star. In essence, we are adding a new start variable and the new start variable ![]() goes to
goes to ![]() .
.
For the following operations, consider a CFL ![]() , and assume that
, and assume that ![]() for some CFG
for some CFG ![]() in Chomsky Normal Form.
in Chomsky Normal Form.
Reversal
When ![]() ,
, ![]() ; and
; and ![]() .
.
For example, let ![]() . Then
. Then ![]() .
.
A derivation of a string in this grammar can be visualized as a binary parse tree, with the left-right traversal of leaves of the tree generating the string ![]() that is derived. A right-left traversal of the leaves of the same tree will generate
that is derived. A right-left traversal of the leaves of the same tree will generate ![]() . Thus a mirror image of the parse tree will generate the reverse of a string. So the following grammar will generate all strings in
. Thus a mirror image of the parse tree will generate the reverse of a string. So the following grammar will generate all strings in ![]() .
.
Form a CFG ![]() where
where ![]() is determined as follows
is determined as follows
 is in
is in 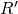 if and only if it is in
if and only if it is in  .
.- For
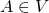 and
and 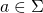 ,
, 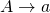 is in
is in 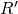 if and only if it is in
if and only if it is in  .
. - For
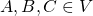 ,
, 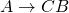 is in
is in 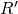 if and only if
if and only if 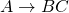 is in
is in  .
.
Then ![]() , so
, so ![]() is context-free.
is context-free.
Prefix
When ![]() ,
, ![]() ; and
; and ![]() .
.
For example, let ![]() . Then
. Then ![]() .
.
Suppose that ![]() has no useless variables, and form a CFG
has no useless variables, and form a CFG ![]() where
where ![]() and
and ![]() is determined as follows
is determined as follows
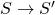 is in
is in 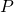 .
.- For
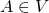 and
and 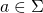 ,
, 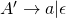 is in
is in 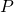 if and only if
if and only if 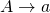 is in
is in  .
. - For
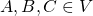 ,
, 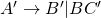 is in
is in 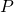 if and only if it
if and only if it 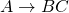 in
in  .
.
Then ![]() , so
, so ![]() is context-free.
is context-free.
To explain this, the original variables generate what they did before. The primed variables generate prefixes of what the original variables generated. We need to keep both because if we had ![]() ,
, ![]() derives
derives ![]() , and
, and ![]() derives
derives ![]() so that
so that ![]() derives
derives ![]() , there may be strings in
, there may be strings in ![]() that are not in
that are not in ![]() . In fact
. In fact ![]() .
.
Subsequence
When ![]() ,
, ![]() and
and ![]() ; and
; and ![]() .
.
For example, let ![]() . Then
. Then ![]() .
.
A derivation using this CNF can be visualized as a binary parse tree, with the left-right traversal of leaves of the tree generating the string ![]() that is derived. In constructing a subsequence, each
that is derived. In constructing a subsequence, each ![]() may be present or absent. Thus, any number of the
may be present or absent. Thus, any number of the ![]() terminals in this string can be replaced by
terminals in this string can be replaced by ![]() to get a subsequence (when the leaves of the parse-tree are traversed left-right) of
to get a subsequence (when the leaves of the parse-tree are traversed left-right) of ![]() . In fact, all possible combinations of doing this will be
. In fact, all possible combinations of doing this will be ![]() . So the following grammar will generate all strings in
. So the following grammar will generate all strings in ![]() .
.
Form a CFG ![]() where
where ![]() is determined as follows
is determined as follows
- For
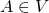 ,
, 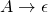 is in
is in 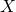 if and only
if and only 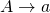 is in
is in  for some
for some 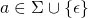 .
.
Then ![]() , so
, so ![]() is context-free.
is context-free.