Decidable languages are closed under complement. If a language is a decidable there is a TM that accepts and halts strings that belong to the language and rejects and halts strings that do not belong to the language. Flipping the accept and reject states generates a TM to decide the complement of this language.
Not all Recognizable languages are closed under complement. If the complement of a recognizable language is also recognizable, the language is, in fact, decidable.
Suppose ![]() is recognizable and
is recognizable and ![]() recognizes
recognizes ![]() . Assume that the complement,
. Assume that the complement, ![]() is also recognizable and
is also recognizable and ![]() recognizes
recognizes ![]() .
.
Here is a decider for ![]()
On input ![]()
- For
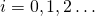
- Run
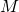 on
on 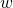 for
for 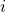 steps. If
steps. If 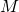 accepts, accept.
accepts, accept. - Run
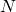 on
on 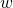 for
for 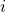 steps. If
steps. If 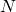 accepts, reject.
accepts, reject.
- Run
Thus, if a language and its complement is recognizable, then the language is decidable.
We know that, ![]() is recognizable but not decidable. This implies that
is recognizable but not decidable. This implies that ![]() is not recognizable.
is not recognizable.