Context-Free Grammar - Formal Definition and Observations

Definition

A Context-Free Grammar (CFG) is a $4$ -tuple

$\begin{equation*} (V, \Sigma, R, S) \end{equation*}$

$V$ – A finite set of variables.

$\Sigma$ – A finite set of terminals. $\epsilon$ is not part of $\Sigma$

$\begin{equation*} V \cap \Sigma = \emptyset \end{equation*}$

$R$ – A finite set of rules. A rule is of the form

$\begin{equation*} A \rightarrow x \text{ , where } A \in V \text{ and }x \in (V \cap \Sigma)^* \end{equation*}$

$S \in V$ – A single start variable.

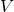$V$ cannot be empty. It must contain the start variable $S$ .
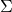$\Sigma$ can be empty. In that case, all the rules will have $\epsilon$ on the RHS.
$R$ can be empty. However, this will define the empty language.