Context-Free Grammars and Parse Trees

The derivation of a string from a Context-Free Grammar (CFG) can be visualized as a parse tree. The root of the parse tree is always the start variable. Each branch corresponds to a rule in the CFG.

Derivations and Parse Trees

Consider the following grammar

$\begin{equation*} S \rightarrow SS | (S) | \epsilon \end{equation*}$

This grammar can produce the string $()()$ using the following derivation

$\begin{equation*} $S \implies SS \implies (S)S \implies ()S \implies ()(S) \implies ()()$ \end{equation*}$

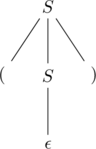
An equivalent parse-tree for the above derivation is

Rendered by QuickLaTeX.com

The same string $()()$ can have another derivation

$\begin{equation*} $S \implies SS \implies S(S) \implies (S)(S) \implies ()(S) \implies ()()$ \end{equation*}$

However, this derivation generates the same parse-tree as above.

Thus, two different derivations may point to the same parse-tree.

Ambiguity

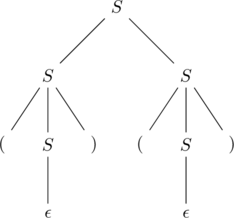
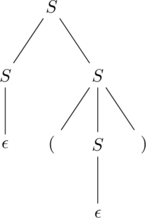
The above grammar can have two different parse trees below to generate $()$ .

Rendered by QuickLaTeX.com

A left-most derivation is a derivation in which the left-most variable is replaced in each step.

Every left-most derivation yields a parse-tree. Every parse-tree yields a left-most derivation. These are in one-to-one correspondence.

A CFG is ambiguous if some string in its language has two or more parse-trees (left-most derivations).

Ambiguity is a property of the grammar, not of the language. Some languages are inherently ambiguous. It is impossible to define an unambiguous grammar for these languages.

Chomsky Normal Form

A CFG in Chomsky Normal Form (CNF) will generate a parse-tree which is a binary tree. This is because each rule is of the form $A \rightarrow BC$ or $A \rightarrow a$ , where $A, B$ and $C$ are variables and $a$ is a terminal.

Each internal node of the binary tree will be a variable. The leaves of the binary tree will be a terminal.

Consider a parse-tree to generate a string of length $n \geq 1$

This parse-tree will have $n$ leaves – one for each symbol in the string. These correspond to $A \rightarrow a$ type rules. A binary tree with $n$ leaves will have $n-1$ internal nodes. These correspond to $A \rightarrow BC$ type rules.