Converting a Context-Free Grammar to a PushDown Automaton

The concept of extended PushDown Automatons can be used to convert a Context-Free Grammar (CFG) to a PushDown Automaton (PDA).

Consider the following CFG

$\begin{equation*} S \rightarrow 0S1S | 1S0S | 0S | S0 | \epsilon | 2S | S2 \end{equation*}$

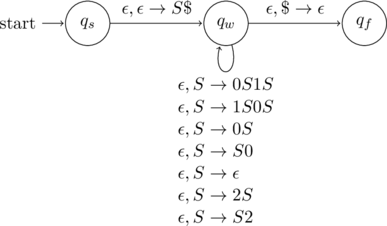
States

The extended PDA will have three states $q_s$ (the start state), $q_w$ (the work state) and $q f$ (the only final state).

$q_0 \rightarrow q_w$

We have to push the $\textdollar$ symbol (indicating the bottom of the stack) and the start variable ( $S$ ) onto the stack. Thus, the transition between these two states will be $\epsilon, \epsilon \rightarrow S \textdollar$ .

$q_w \rightarrow q_f$

We have to check for the bottom of the stack. Thus, the transition between these two states will be $\epsilon, \textdollar \rightarrow \epsilon$ .

Rules as transitions

For every rule of the type $A \rightarrow w$ , add the transition $\epsilon, A \rightarrow w$ that loops on $q_w$ .

Rendered by QuickLaTeX.com

In essence, these transitions simulate an application of a rule.

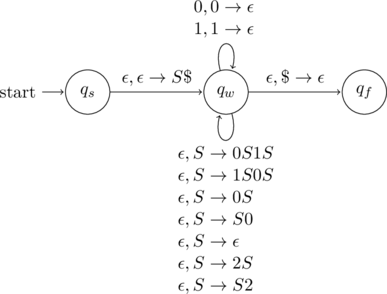
Terminals as transitions

For any $a \in \Sigma$ , add the transition $a, a \rightarrow \epsilon$ that loops on $q_w$ .

Rendered by QuickLaTeX.com

The reason this transition is added is to match the terminals generated by the CFG rules with the symbols the PDA reads.

The difference between PDAs and CFGs is that the former reads a string while the the latter generates a string. For the PDA to accept a string, it needs to read the symbols in the strings that can be generated by the PDA.

Conversion to PDA

The extended PDA transitions can be broken down into just PDA transitions by following the steps outlined here.

The Beard Sage