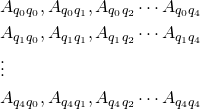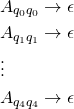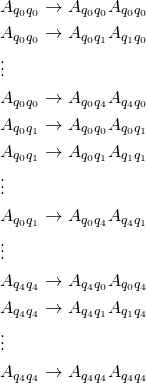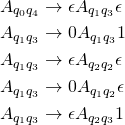Converting a PushDown Automaton (PDA) into an equivalent Context-Free Grammar (CFG) is quite involved. Consider the following PDA
Modify the PDA
The first step is to modify this PDA to satisfy the following
- The PDA must have a single final state.
- The PDA must accept a string with an empty stack.
- Every transition of the PDA either pops or pushes but not both.
1 and 2 are already satisfied. To satisfy 3, the PDA is modified as follows
Now the PDA is ready to be converted to an equivalent CFG.
Variables
The CFG will have variables of the type ![]() where
where ![]() and
and ![]() are states in the PDA. Thus, a PDA with
are states in the PDA. Thus, a PDA with ![]() states will have
states will have ![]() variables. Here are the variables for the above PDA.
variables. Here are the variables for the above PDA.
The start variable will be ![]() . In this case –
. In this case – ![]() .
.
Rules
First add rules of the type ![]() for all states
for all states ![]() in the PDA. Thus, a PDA with
in the PDA. Thus, a PDA with ![]() states will have
states will have ![]() rules of this type. Here are those rules.
rules of this type. Here are those rules.
Next, add rules of the type ![]() for all states
for all states ![]() ,
, ![]() and
and ![]() in the PDA. Thus, a PDA with
in the PDA. Thus, a PDA with ![]() states will have
states will have ![]() rules of this type. Here are those rules.
rules of this type. Here are those rules.
Finally, add rules of the type ![]() where there is a transition from
where there is a transition from ![]() to
to ![]() on reading
on reading ![]() and a transition from
and a transition from ![]() to
to ![]() on reading
on reading ![]() . The number of rules of this type depends on the PDA. Here are those rules
. The number of rules of this type depends on the PDA. Here are those rules