A language is decidable if there is a Turing Machine that halts and accepts strings that belong to the language, and halts and rejects strings that do not belong to the language.

EQ_DFA

There exists a TM that decides the above language. Given the string encoding of two DFAs and , a TM can decide whether the languages of the two DFAs are the same.

High-Level Description

On input

1. Check whether 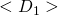and 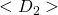indeed encode a DFA. If not, reject.
2. Construct a DFA, , for
3. Run on .

The idea behind this approach is this: if two DFAs have the same language their union and intersection will be the same. Thus, .

This extends to NFAs and regular expressions as well. Basically, the equivalence of regular languages is decidable as the problem can be reduced to .