Models that assign probabilities to sequences of words are called language models. An ![]() –gram is a sequence of
–gram is a sequence of ![]() words: a
words: a ![]() -gram (or bigram) is a two-word sequence of words like “please turn”, “turn your”, or “your homework”, and a
-gram (or bigram) is a two-word sequence of words like “please turn”, “turn your”, or “your homework”, and a ![]() -gram (or trigram) is a three-word sequence of words like “please turn your”, or “turn your homework”.
-gram (or trigram) is a three-word sequence of words like “please turn your”, or “turn your homework”.
Notation
To represent the probability of a particular random variable ![]() taking on the value “the”, or
taking on the value “the”, or ![]() , use the simplification
, use the simplification ![]() .
.
A sequence of ![]() words is represented either as
words is represented either as ![]() or
or ![]() .
.
Probability of a Sequence
For the joint probability of each word in a sequence having a particular value ![]() use
use ![]() .
.
The intuition of the ![]() -gram model is that instead of computing the probability of a word given its entire history, approximate the history by just the last few words.
-gram model is that instead of computing the probability of a word given its entire history, approximate the history by just the last few words.
Bigram
The bigram model, for example, approximates the probability of a word given all the previous words ![]() by using only the conditional probability of the preceding word
by using only the conditional probability of the preceding word ![]() .
.
This assumption that the probability of a word depends only on the previous word is also called a Markov assumption.
Thus, for a bigram
N-gram
The ![]() -gram (which looks
-gram (which looks ![]() words into the past) approximates the probability as follows
words into the past) approximates the probability as follows
Parameter Estimation
Maximum Likelihood estimation is used to compute the parameters of an ![]() -gram model. This process involves getting counts from a corpus, and normalizing the counts so that they lie between
-gram model. This process involves getting counts from a corpus, and normalizing the counts so that they lie between ![]() and
and ![]() .
.
To compute a particular bigram probability of a word ![]() given a previous word
given a previous word ![]() , compute the count of the bigram
, compute the count of the bigram ![]() and normalize by the sum of all the bigrams that share the same first word
and normalize by the sum of all the bigrams that share the same first word ![]()
The sum of all bigram counts that start with a given word ![]() must be equal to the unigram count for that word
must be equal to the unigram count for that word ![]() .
.
For the general case of MLE ![]() -gram parameter estimation:
-gram parameter estimation:
Perplexity
The perplexity (sometimes called ![]() for short) of a language model on a test set is the inverse probability of the test set, normalized by the number of words. The higher the conditional probability of the word sequence, the lower the perplexity. Consider the test set
for short) of a language model on a test set is the inverse probability of the test set, normalized by the number of words. The higher the conditional probability of the word sequence, the lower the perplexity. Consider the test set ![]() .
.
For a bigram language model
The more the information the ![]() -gram gives about a word sequence, the lower the perplexity.
-gram gives about a word sequence, the lower the perplexity.
Smoothing
Smoothing is a technique to prevent a language models from assigning zero probability to unseen events.
The unsmoothed Maximum Likelihood Estimate of the unigram probability of the word ![]() is its count
is its count ![]() normalized by the total number of word tokens
normalized by the total number of word tokens ![]() .
.
Laplace (add-one) Smoothing technique adds a one to all the bigram counts. Since there are ![]() words in the vocabulary and each one was incremented, the denominator needs to be adjusted to take into account the extra
words in the vocabulary and each one was incremented, the denominator needs to be adjusted to take into account the extra ![]() observations.
observations.
Comparing the two equations above
The adjusted count ![]() describes how the smoothing affects the numerator.
describes how the smoothing affects the numerator.
The bigram probabilities follow the same technique
An extension of the above technique is to add ![]() instead of
instead of ![]() .
.
Interpolation
Interpolation is an approach to mix the probability estimates from all the ![]() -gram estimators. The trigram, bigram, and unigram counts are weighed and combined. An example of simple linear interpolation is given below
-gram estimators. The trigram, bigram, and unigram counts are weighed and combined. An example of simple linear interpolation is given below
such that

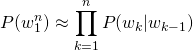

![Rendered by QuickLaTeX.com \begin{equation*} PP(W) = P(w_1w_2 \cdots w_N)^{-\frac{1}{N}} = \sqrt[N]{\frac{1}{P(w_1w_2 \cdots w_N)}} = \sqrt[N]{\prod_{i=1}^{N}\frac{1}{P(w_i|w_1 \cdots w_{i-1})}} \end{equation*}](http://thebeardsage.com/wp-content/ql-cache/quicklatex.com-deec9aac0f98b67f2732783f5426b714_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} PP(W) = \sqrt[N]{\prod_{i=1}^{N}\frac{1}{P(w_i|w_{i-1})}} \end{equation*}](http://thebeardsage.com/wp-content/ql-cache/quicklatex.com-c07bc194ac5bcc8c893143b225efde41_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} P_{\text{Laplace}}(w_n|w_{n-1}) &= \frac{C(w_{n-1}w_n) + 1}{\sum_w(C(w_{n-1}w) + 1)} = \frac{C(w_{n-1}w_n) + 1}{C(w_{n-1}) + V} \\ c^*(w_n|w_{n-1}) &= \frac{[C(w_{n-1}w_n) + 1] \cdot C(w_{n-1})}{C(w_{n-1}) + V} \end{align*}](http://thebeardsage.com/wp-content/ql-cache/quicklatex.com-29629b4dc55c9a430c6b090732176cf6_l3.png)