Proving a Language is not Regular using the Pumping Lemma - String Choices

Consider the following language definition

$\begin{equation*} L = \{w \in \{0, 1, 2\}^* : w \text{ contains equal number of $01$ and $10$ substrings}\} \end{equation*}$

This language is not regular. Applying the pumping lemma to prove that this language is not regular is not straightforward. This is because every string in $L$ can be pumped if it has length at least $p$ .

Pump-able Strings

Pick any string $s \in L$ with $|s| \geq p$ . According the pumping lemma $s$ can be written as $xyz$ and $xy^iz \in L$ for all $i \geq 0$ .

Look at short prefixes of $s$ – the symbols that lie at the start of the string. For each of these prefixes, a possible split of $s$ into $xyz$ is given below.

Prefix	$x$	$y$	$z$
$2$	$\epsilon$	$2$	rest of the string
$00$	$\epsilon$	$0$	$0 +$ rest of the string
$010$	$\epsilon$	$01$	$0 +$ rest of the string
$011$	0	$1$	$1 +$ rest of the string
$012$	$\epsilon$	$01$	$2 +$ rest of the string
$100$	$1$	$0$	$0 +$ rest of the string
$101$	$\epsilon$	$10$	$1 +$ rest of the string
$102$	$\epsilon$	$10$	$2 +$ rest of the string
$11$	$\epsilon$	$1$	$1 +$ rest of the string

All possible prefixes have been taken into account. For all these case, pumping up $y$ will add equal number of $01$ and $10$ substrings. Thus, the string remains in the language.

Closure under Intersection

Suppose to the contrary $L$ is regular. Then $L' = L \cap (012 \cup 102)^*$ is regular by closure under intersection. If $L'$ is proved to be not regular then the assumption that $L$ is regular is wrong. Thus, the problem is reduced to proving that $L'$ is not regular.

Using the Pumping Lemma on 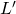$L'$

Note that the length of every string in $L'$ is a multiple of $3$ .

Let $p$ be the pumping length for $L'$ . Choose $s = (012)^p(102)^p$ .

Then $s \in L'$ (it has $p$ occurrences of $01$ and $p$ occurrences of $10$ ) and $|s| = 6p \geq p$ , so the pumping lemma applies.

Consider all ways to write $s = xyz$ with $|xy| \leq p$ and $|y| > 0$ . Because $xy$ is a prefix of $s$ , it is a prefix of $(012)^p$ . Thus, $y$ is a nonempty substring of $(012)^p$ .

Write $|y| = a$ and observe that $a \geq 1$ .

Case 1

$a$ is not a multiple of $3$ .

Then $|xy^2 z| = 6p + a$ . Because $6p + a$ is not a multiple of $3$ , $xy^2 z$ cannot belong to $L'$ , which is a contradiction.

Case 2

$a$ is a multiple of $3$ .

Say $a = 3b$ with $b \geq 1$ . Then $y$ is one of $(012)^b$ , $2(012)^{b-1}01$ , or $12(012)^{b-1}0$ . For each, $xy^2 z$ has $p + b$ occurrences of $01$ and $p$ occurrences of $10$ , so is not in $L'$ , a contradiction.