Every non-trivial property, ![]() , of the language of Turing Machines is undecidable. This is Rice’s Theorem.
, of the language of Turing Machines is undecidable. This is Rice’s Theorem.
Because ![]() is non-trivial there is some Turing Machine
is non-trivial there is some Turing Machine ![]() such that
such that ![]() and some other Turing Machine
and some other Turing Machine ![]() such that
such that ![]() .
.
Proof
![]() is undecidable. This can be proved using contradiction.
is undecidable. This can be proved using contradiction.
Suppose to the contrary that that there exists a TM, ![]() , that decides
, that decides ![]() . This machine takes
. This machine takes ![]() as an input. It accepts if
as an input. It accepts if ![]() and rejects otherwise.
and rejects otherwise.
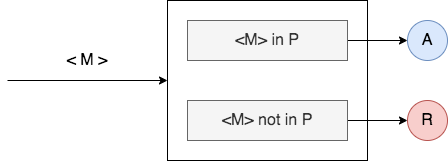

Using ![]() , build another TM
, build another TM ![]() as follows
as follows
On input ![]()
- Construct a new TM
 as follows
as follows- On input
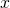 , Run
, Run 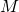 on
on 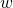 .
. - If
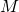 accepts
accepts 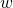 , run
, run  on
on 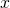 .
. - If
 accepts
accepts 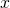 , accept.
, accept.
- On input
- Run
 on
on  . If
. If  accepts
accepts  (implying that
(implying that  has property
has property 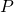 ), accept. Else, reject.
), accept. Else, reject.
The machine ![]() takes
takes ![]() as an input. It accepts if
as an input. It accepts if ![]() satisfies the property
satisfies the property ![]() . This implies that
. This implies that ![]() and
and ![]() share the same language. This will only hold true if
share the same language. This will only hold true if ![]() accepts
accepts ![]() . In essence, this is a machine that decides
. In essence, this is a machine that decides ![]() . We say that
. We say that ![]() reduces to
reduces to ![]() .
.
Since ![]() is undecidable, the property
is undecidable, the property ![]() is also undecidable.
is also undecidable.
Example
Using Rice’s theorem makes the problem of proving the undecidability of languages pretty straightforward. You have to identify the property and prove that it is non-trivial. Consider the following problem
The property ![]() in this case is
in this case is ![]() is context-free.
is context-free. ![]() is indeed a property of the language of TMs because for any 2 machines
is indeed a property of the language of TMs because for any 2 machines ![]() and
and ![]() such that
such that ![]()
![]() is non-trivial because there is at least one TM that belongs to
is non-trivial because there is at least one TM that belongs to ![]() (a TM that accepts
(a TM that accepts ![]() ) and at least one TM that doesn’t belong to
) and at least one TM that doesn’t belong to ![]() (a TM that accepts
(a TM that accepts ![]() ).
).
By Rice’s Theorem, ![]() is undecidable.
is undecidable.