The Markov Property - The Beard Sage

The Markov Property makes a very strong assumption that the output of a random variable in a sequence only depends on the current state. Consider a sequence of state variables $q_1, q_2, \cdots, q_i$ . The Markov assumption states that

$\begin{equation*}P(q_i = a | q_1 q_2 \cdots q_{i-1}) = P(q_i = a | q_{i-1})\end{equation*}$

A discrete-time process satisfying this property is called a Markov Chain and a continuous process is called a Markov process.

Markov Chain

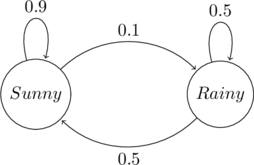
A Markov Chain is defined by a state space and the probabilities of transitioning within this state space. Given $n$ states there are $n^2$ possible transitions. This can be represented as a finite state machine with the symbols above the transition indicating the probability of that transition.

Consider the discrete process of predicting the weather for a given day. The set of values it can take include $\{Sunny, Rainy\}$ . These correspond to the states. Each discrete quanta is one day.

Rendered by QuickLaTeX.com

The Markov assumption states that today’s weather depends only on yesterday’s weather. Assume that there is a high chance that today will be $Sunny$ if yesterday was $Sunny$ and a moderate chance that today will be $Rainy$ if yesterday was $Rainy$ . These values are added as probabilities. The outgoing probabilities of a state must add up to $1$ .

Rendered by QuickLaTeX.com

Using this Markov Chain, the weather can be predicted by following the transitions. A test run will result in the following output. $S$ stands for $Sunny$ and $R$ stands for $Rainy$

$\begin{equation*}\cdots S \, S \, S \, S \, S \, R \, R \, S \, S \, S \, S \, S \, S \cdots\end{equation*}$

Memoryless

The Markov property makes the model memoryless. The sequence of states generated are not context-sensitive and do not rely on the information captured in the full chain of prior states. For example, a Markov chain would do a poor job in mimicking the musical structure of a song. Higher order Markov chains use the assumption of the current state relying on multiple prior states.

Mathematical Representation

A Markov Chain can be mathematically represented as transition matrix. Given $n$ possible states, the matrix will have dimensions $n \times n$ , where each entry $p_{ij}$ is the probability of transitioning from $i$ to $j$ . Also, by the law of total probability

$\begin{equation*}\sum_{j=0}^{n} p_{ij} = 1\end{equation*}$

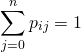
The Markov chain also has an initial state vector of dimensions $n \times 1$ , where each entry $p_j$ is the probability of starting at the $j$ -th state.

Markov Chain

Memoryless

Mathematical Representation

Leave a Reply Cancel reply