In a sparse matrix, the elements of a vector are usually stored in some compacted form and then accessed indirectly. This compact form is called the index vector. It only keeps track of the useful indices within a vector.

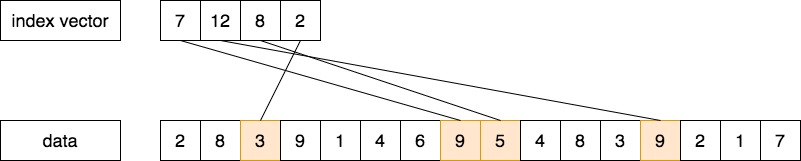
The primary mechanism for supporting sparse matrices is gather-scatter operations using index vectors. The goal of such operations is to support moving between a compressed representation (i.e., zeros are not included) and normal representation (i.e., the zeros are included) of a sparse matrix.

A gather operation takes an index vector and fetches the vector whose elements are at the addresses given by adding a base address to the offsets given in the index vector. The result is a dense vector in a vector register.

After these elements are operated on in dense form, the sparse vector can be stored in expanded form by a scatter store, using another index vector.

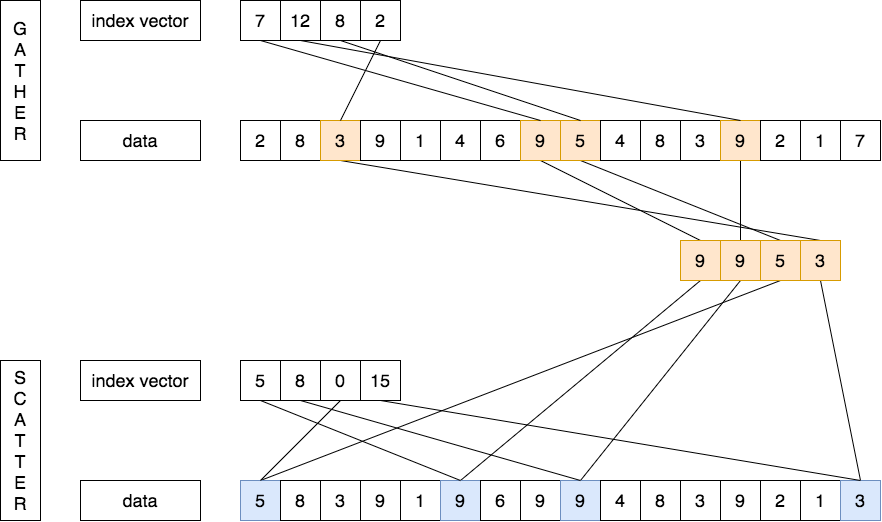
The advantage of this mode is, that every element can be retrieved using a dedicated index. Disadvantage is that the indexing this way might completely destroy hardware based memory prefetching, and in turn negatively impact your performance. Also, mind that all elements might be far away, meaning that more cachelines have to be moved to the lowest cache level.

Scatter-gather operations can also be used to access vector data that is not stored in a strided fashion in memory.

Although indexed loads and stores (gather and scatter) can be pipelined, they typically run much more slowly than non-indexed loads or stores, since the memory banks are not known at the start of the instruction. Each element has an individual address, so they can’t be handled in groups, and there can be conflicts at many places throughout the memory system. Thus, each individual access incurs significant latency.