A block is the minimum unit of information that can be either present or not present in a cache. A block in the main memory is called a frame and a block in the cache memory is called a cache block or a cache line.
A processor accesses data within a frame or cache block through an addressing system. The smallest chunk of information that the processor can read is in units of words.

The main and cache memory are each divided into frames/blocks of ![]() words. When data is moved into the cache an entire frame of
words. When data is moved into the cache an entire frame of ![]() words occupies one block of
words occupies one block of ![]() words in the cache.
words in the cache.
If the main memory address ![]() contains
contains ![]() bits, and the least significant
bits, and the least significant ![]() bits are used to represent the
bits are used to represent the ![]() words in each frame/block, the remaining
words in each frame/block, the remaining ![]() bits of the address form the tag for the block, whereby the tag is the beginning address of the block of
bits of the address form the tag for the block, whereby the tag is the beginning address of the block of ![]() words. Thus
words. Thus ![]() bits can reference any frame from
bits can reference any frame from ![]() to
to ![]() in the main memory.
in the main memory.
The cache capacity is ![]() blocks. The data area of the cache has a total capacity of
blocks. The data area of the cache has a total capacity of ![]() words. The cache also has a tag area consisting of
words. The cache also has a tag area consisting of ![]() tags. Each tag in the tag area identifies the address range of the
tags. Each tag in the tag area identifies the address range of the ![]() words in the corresponding block in the cache.
words in the corresponding block in the cache.
When the processor references a primary memory address ![]() , the cache mechanism compares the tag portion of
, the cache mechanism compares the tag portion of ![]() to each tag in the tag area. The least significant
to each tag in the tag area. The least significant ![]() bits of
bits of ![]() are used to select the appropriate word from the block, to be transmitted to the processor.
are used to select the appropriate word from the block, to be transmitted to the processor.
Examples
| Word Size | # Words in a Block | Bits to reference Word within a Block | Primary Memory | Bits to reference Primary Memory | Tag Length | Cache Memory | # of Cache Blocks |
Fully Associative Mapping
In the above mapping scheme one frame can occupy any of the cache blocks. This is called a fully associative mapping scheme. All the ![]() tags must be searched in order to determine a hit/miss.
tags must be searched in order to determine a hit/miss.
Direct Mapping
On the other extreme, in a direct mapping each memory address ![]() maps to a unique cache block. Use the least significant
maps to a unique cache block. Use the least significant ![]() bits of the tag to indicate the cache block in which a frame can reside. The tag search is now reduced to just one comparison.
bits of the tag to indicate the cache block in which a frame can reside. The tag search is now reduced to just one comparison.
| Address | Tag | Block number | Word number |
This mapping divides the ![]() addresses in the main memory into
addresses in the main memory into ![]() partitions. Thus,
partitions. Thus, ![]() addresses map to the same cache block. The addresses that map to the same cache block are
addresses map to the same cache block. The addresses that map to the same cache block are ![]() words apart in main memory.
words apart in main memory.

 blocks, the frames that map to the same cache block are
blocks, the frames that map to the same cache block are  frames apart.
frames apart.- Word Size
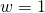 B
B - Cache Size
 B
B - Number of Blocks in Cache
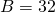
- Bits to reference a block
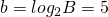
- Size of one Block/Frame
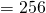 B
B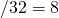 B
B - Words per Block/Frame
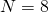 B
B B
B 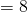
- Bits to reference Word within a block
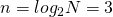
- Primary Memory
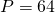 KB
KB - Bits to reference Primary Memory

- Number of Frames in Primary Memory
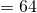 KB
KB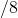 B
B 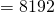
- Tag length
 .
.
Set Associative Mapping
A compromise between the two types of mapping is called set-associative mapping. The ![]() cache blocks are divided into
cache blocks are divided into ![]() partitions each containing
partitions each containing ![]() blocks. This is called a
blocks. This is called a ![]() -way set-associative mapping.
-way set-associative mapping.
| Address | Tag | Set number | Word number |
This mapping divides the main memory into ![]() partitions. Each frame can now reside in of the
partitions. Each frame can now reside in of the ![]() corresponding cache blocks, known as a set. The tag search is now limited to
corresponding cache blocks, known as a set. The tag search is now limited to ![]() tags in the set.
tags in the set.

 blocks, the frames that map to the same set are
blocks, the frames that map to the same set are  frames apart.
frames apart.- Word Size
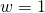 B
B - Bits to reference Word within a block
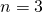
- Words per Block/Frame

- Size of one Block/Frame
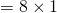 B
B 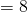 B
B - Number of slots in a set
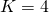
- Size of one set
 B
B 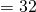 B
B - Number of Sets in Cache
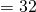
- Bits to reference a set
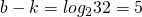
- Cache Size
 B
B 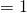 KB
KB - Primary Memory
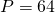 KB
KB - Bits to reference Primary Memory

- Number of Frames in Primary Memory
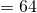 KB
KB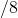 B
B 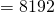
- Tag length
 .
.
Observations
![]() implies direct mapping.
implies direct mapping.
![]() implies fully associative mapping.
implies fully associative mapping.
A direct-mapped cache is simply a one-way set-associative cache: each cache entry holds one block and each set has one element. A fully associative cache with ![]() entries is simply an
entries is simply an ![]() -way set-associative cache; it has one set with
-way set-associative cache; it has one set with ![]() blocks, and an entry can reside in any block within that set.
blocks, and an entry can reside in any block within that set.
Increasing the degree of associativity usually decreases the miss rate, with a potential increase in the hit time. While the benefit of going from one-way to two-way set associative is significant, the benefits of further associativity are smaller.
Each increase by a factor of ![]() in associativity doubles the number of blocks per set and halves the number of sets. Each factor of
in associativity doubles the number of blocks per set and halves the number of sets. Each factor of ![]() increase in associativity decreases the size of the index by
increase in associativity decreases the size of the index by ![]() bit and increases the size of the tag by
bit and increases the size of the tag by ![]() bit.
bit.

Total size of cache in blocks = Number of sets ![]() Associativity
Associativity