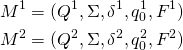The Cross-Product of ![]() DFAs is a single DFA which simulates the operation of the
DFAs is a single DFA which simulates the operation of the ![]() DFAs in parallel. For the sake of simplicity it is assumed that the DFAs share the same alphabet
DFAs in parallel. For the sake of simplicity it is assumed that the DFAs share the same alphabet ![]() .
.
Problem Statement
Let the two DFAs be defined by ![]() and
and ![]()
The languages accepted by these DFAs are ![]() and
and ![]() respectively. Using the Cross-Product, a single DFA can be constructed that recognizes
respectively. Using the Cross-Product, a single DFA can be constructed that recognizes
Cross-Product
The DFA constructed via Cross-Product is defined as follows
where
and
| Operation | |
|---|---|
Example Problem
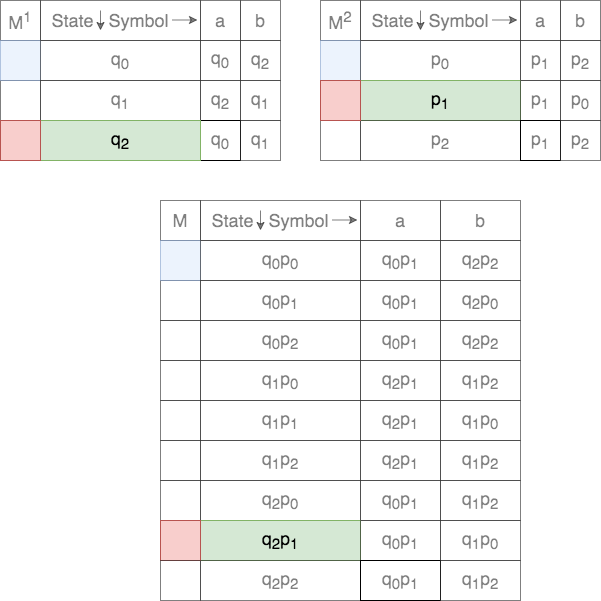
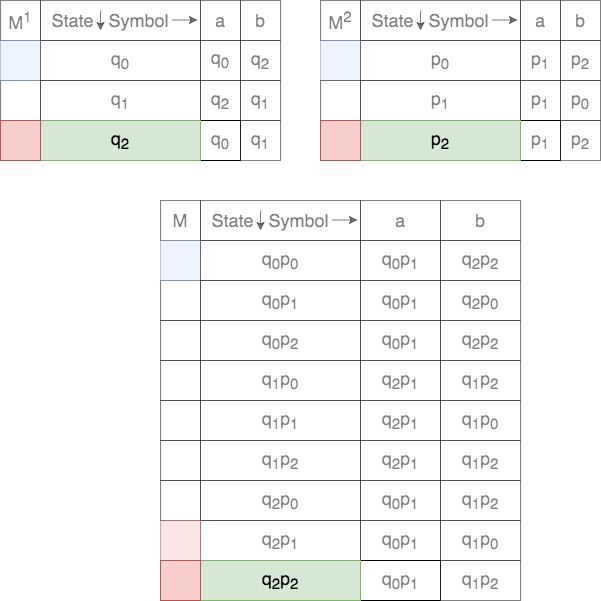
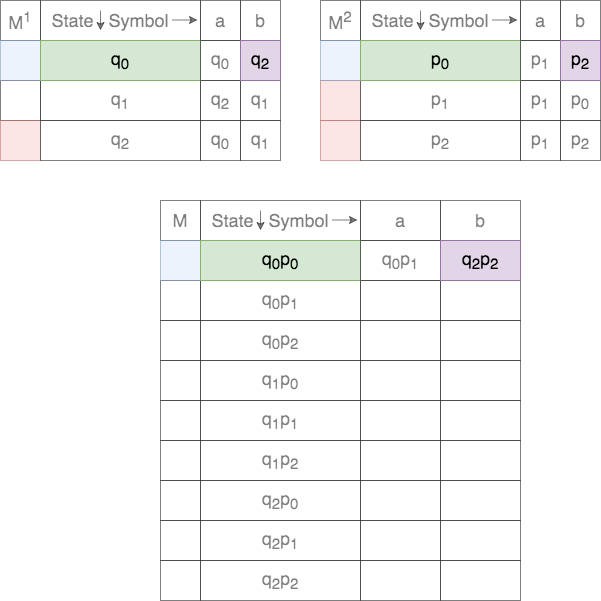
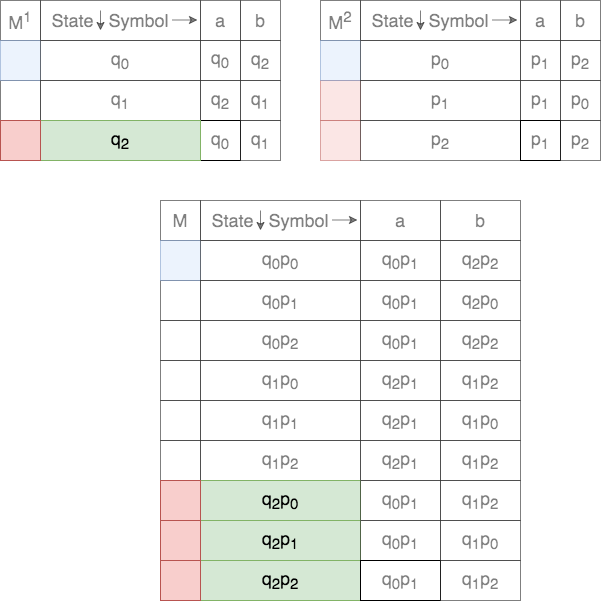
It is much easier to follow the Cross-Product construction by writing down the formal definition as a transition table. Consider the two DFAs shown below. The alphabet ![]() . The blue color indicates the start state and the red color indicate(s) the final state(s).
. The blue color indicates the start state and the red color indicate(s) the final state(s).
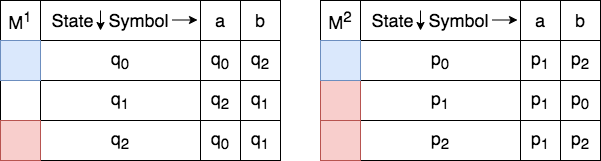
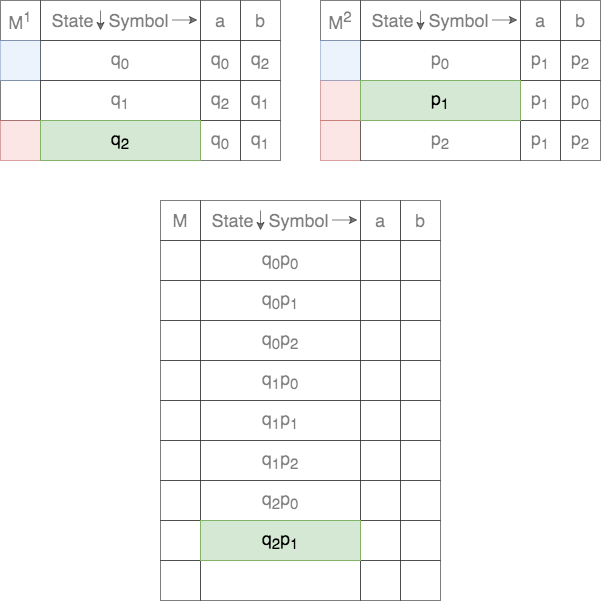
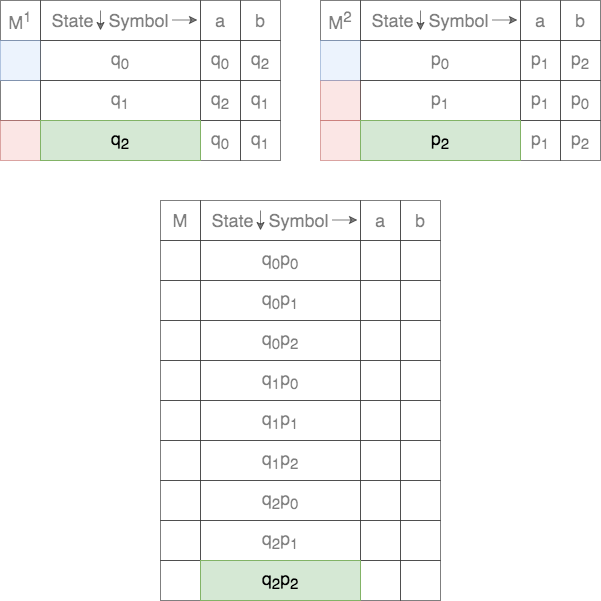
The set of states ![]() for the Cross-Product is defined as
for the Cross-Product is defined as
Thus, each state in ![]() is a tuple. The first element comes from the set of states of the first DFA and the second element from the set of states of the second DFA. Thus, there will be a total of
is a tuple. The first element comes from the set of states of the first DFA and the second element from the set of states of the second DFA. Thus, there will be a total of ![]() states in
states in ![]() . These are populated as follows
. These are populated as follows
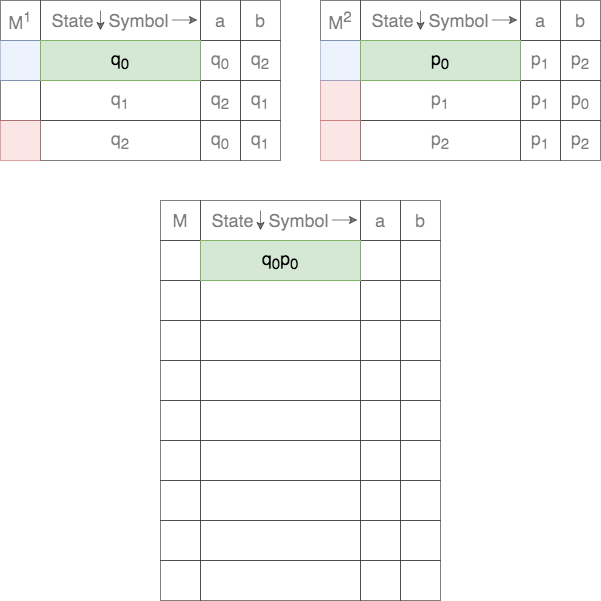
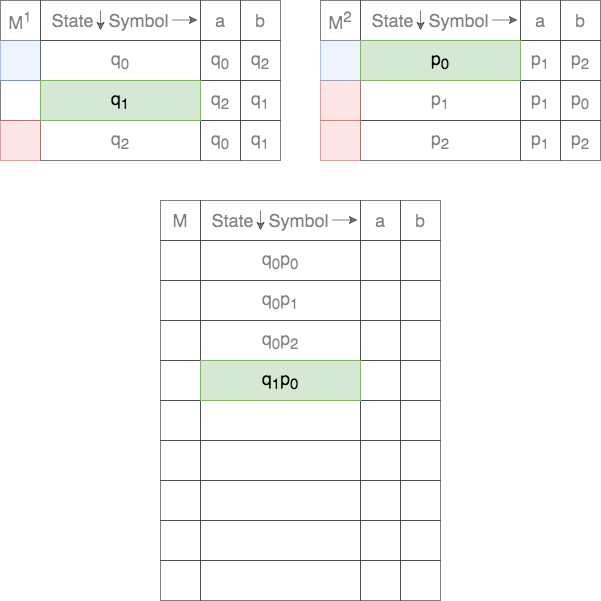
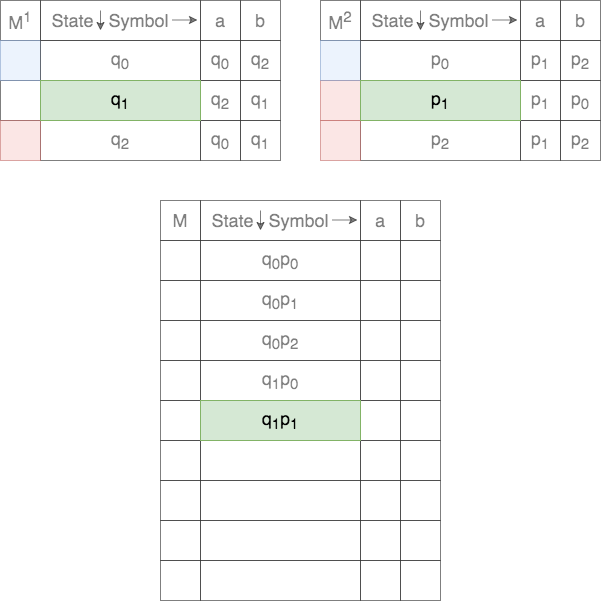
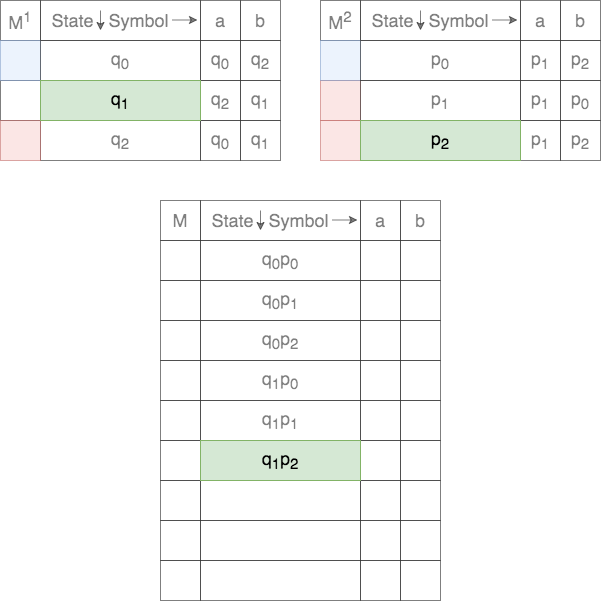
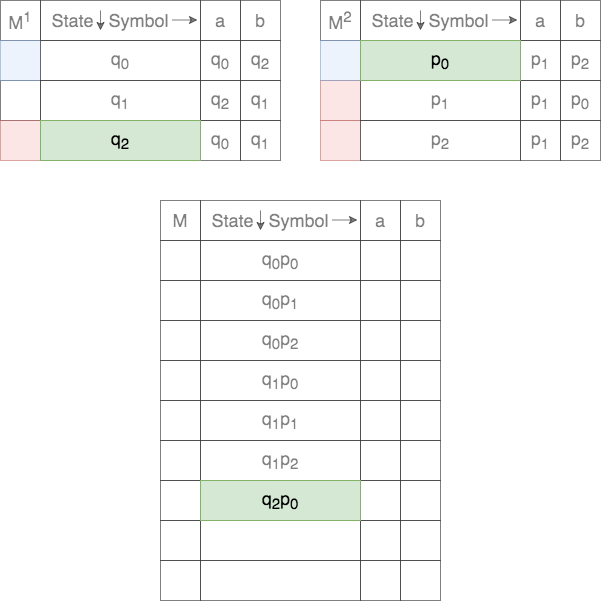
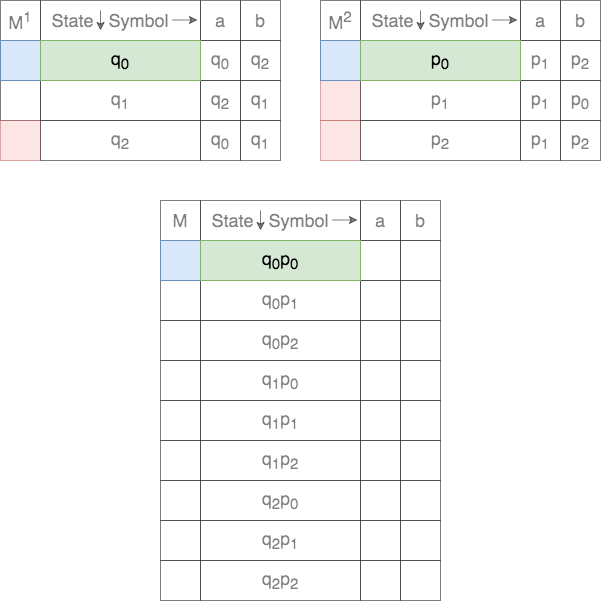
The start state, ![]() , for the Cross-Product is defined as
, for the Cross-Product is defined as
Thus, the start state, ![]() , is a tuple. The first element is the start state of the first DFA and the second element is the start state of the second DFA.
, is a tuple. The first element is the start state of the first DFA and the second element is the start state of the second DFA.
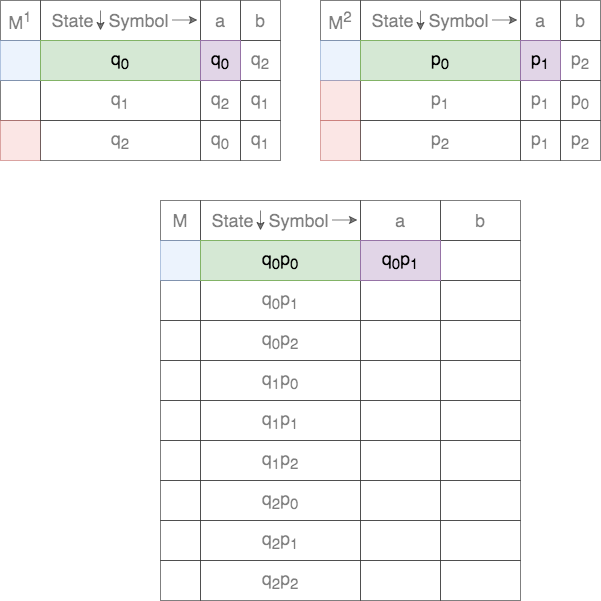
The transition function, ![]() , for the Cross-Product is defined as
, for the Cross-Product is defined as
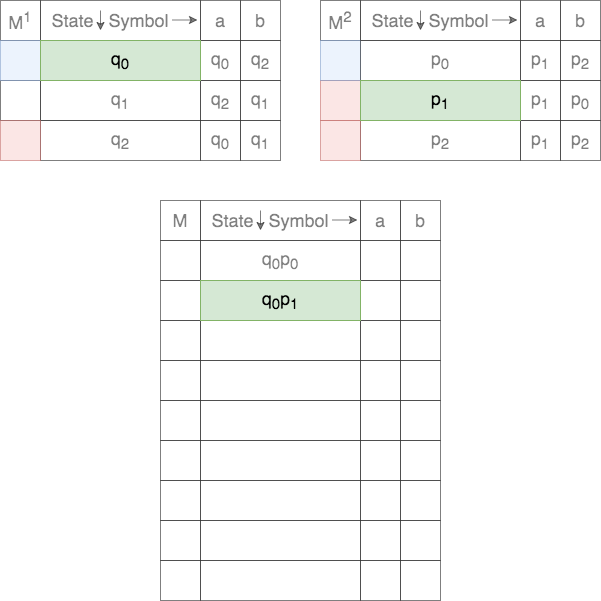
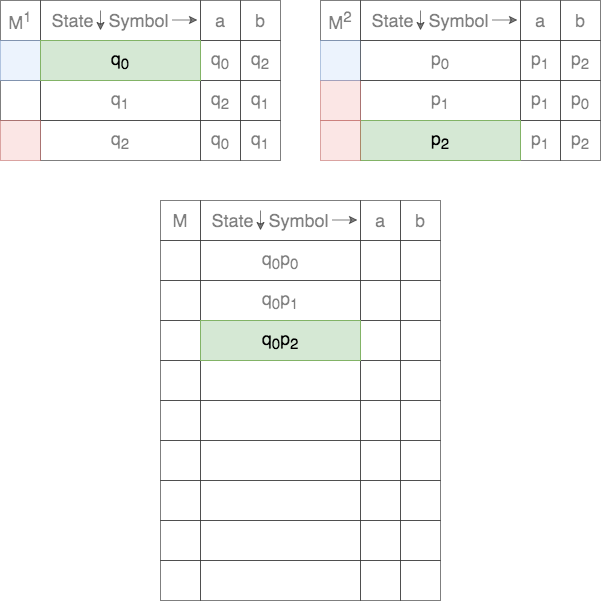
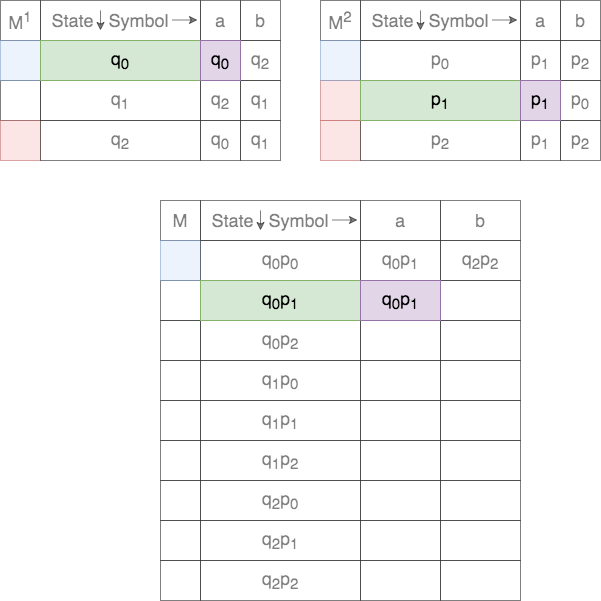
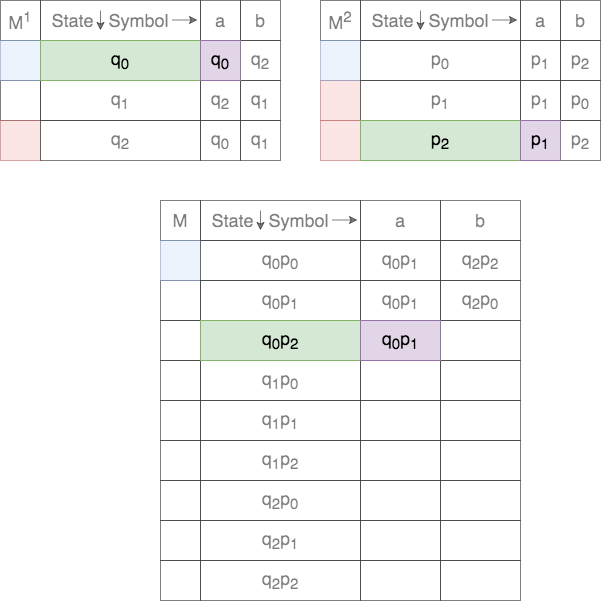
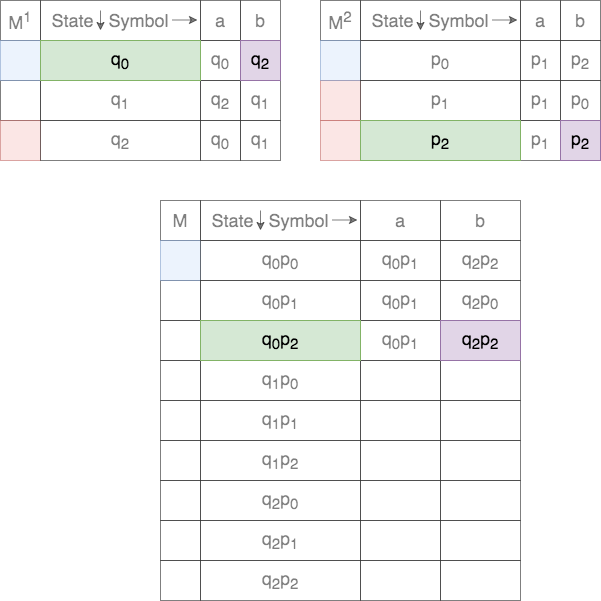
Thus, for a given tuple of states, the transition for each of the states on the two DFAs are tracked. This process is shown below.

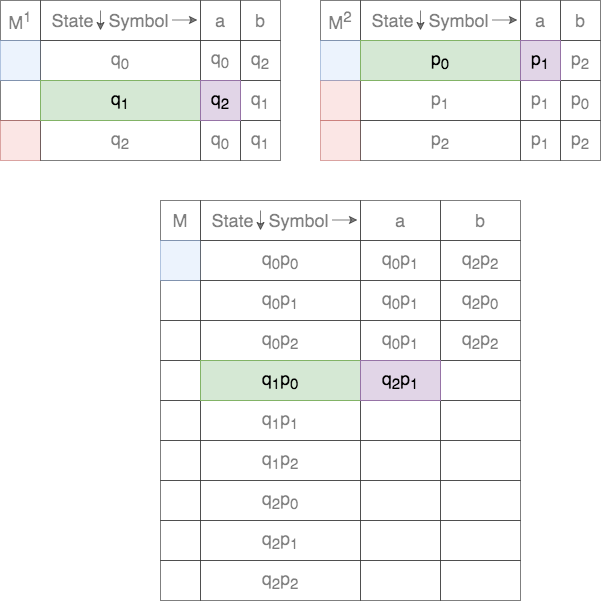
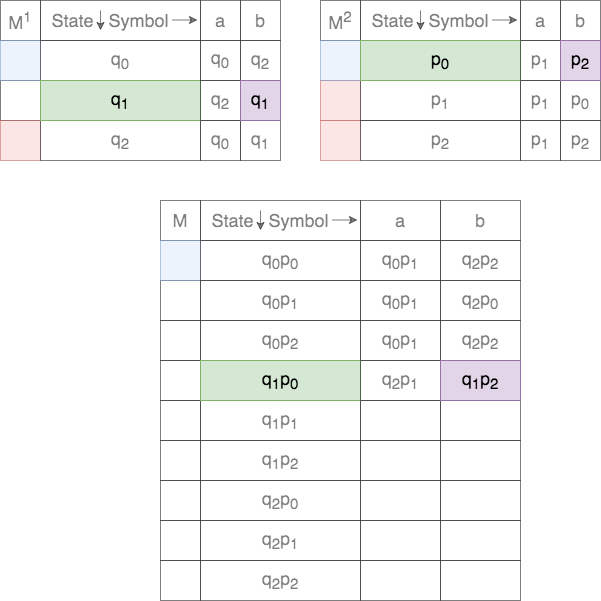
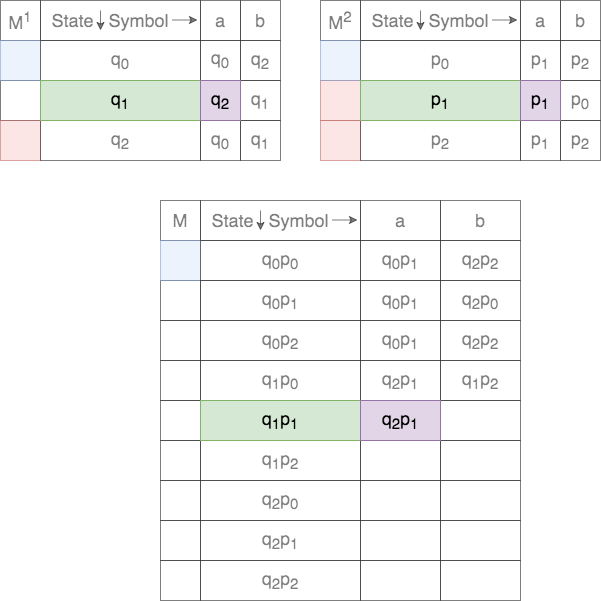
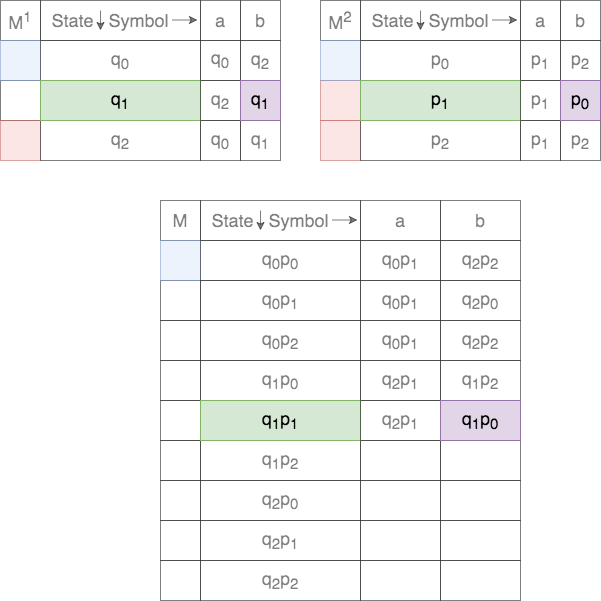
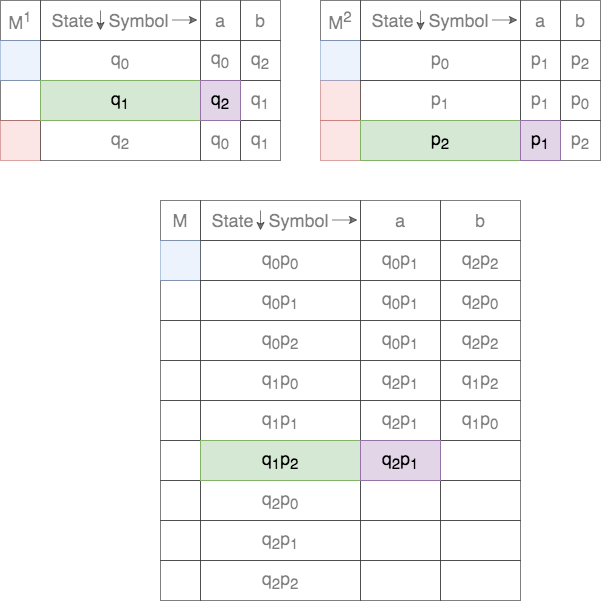
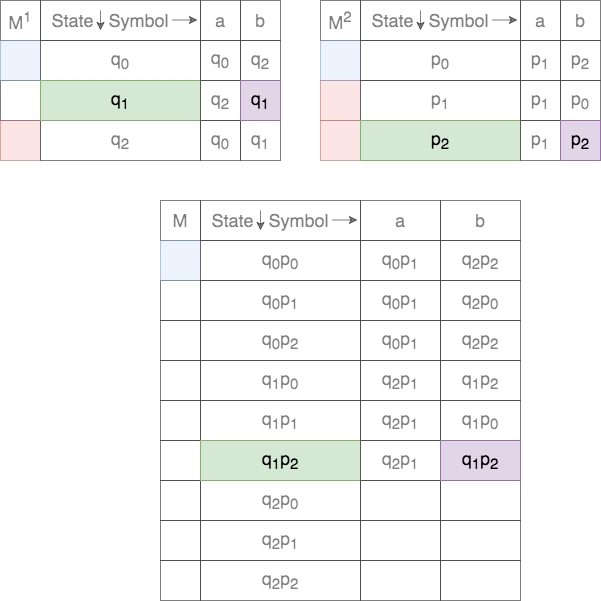
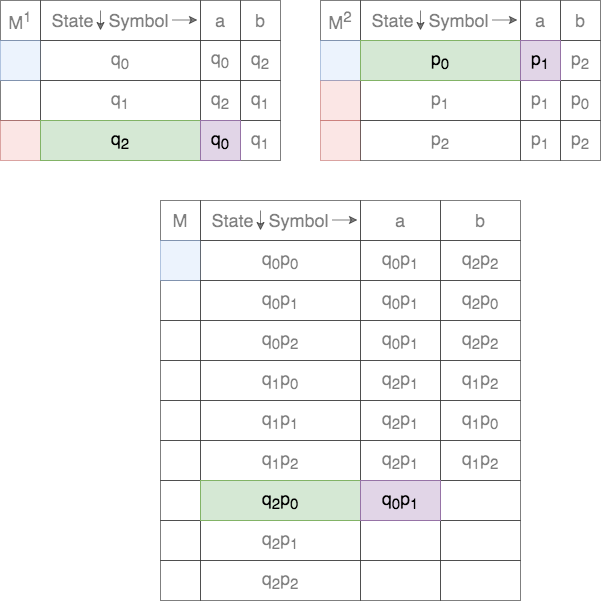
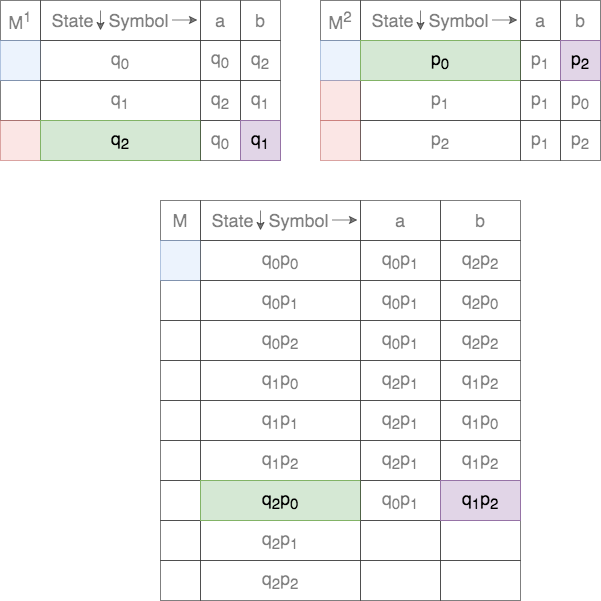
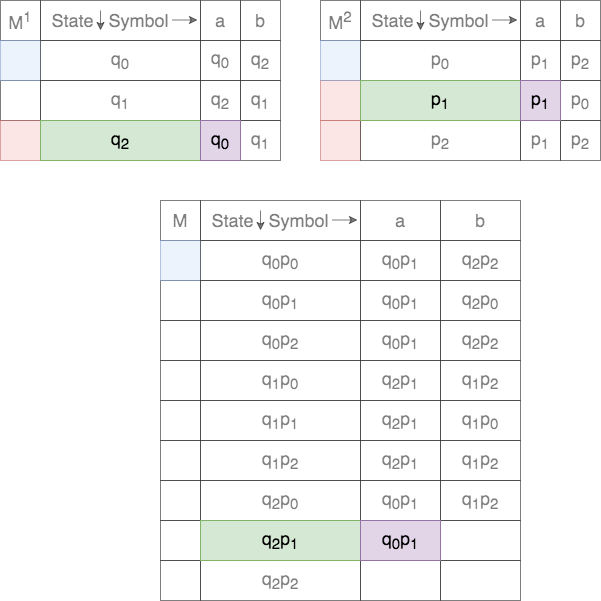
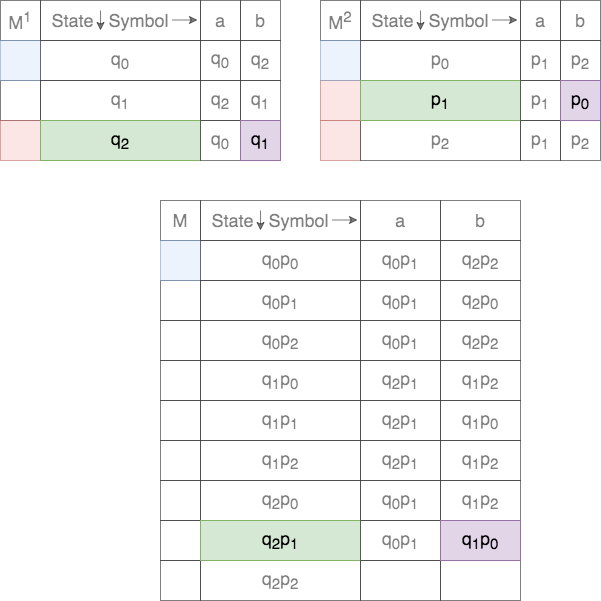
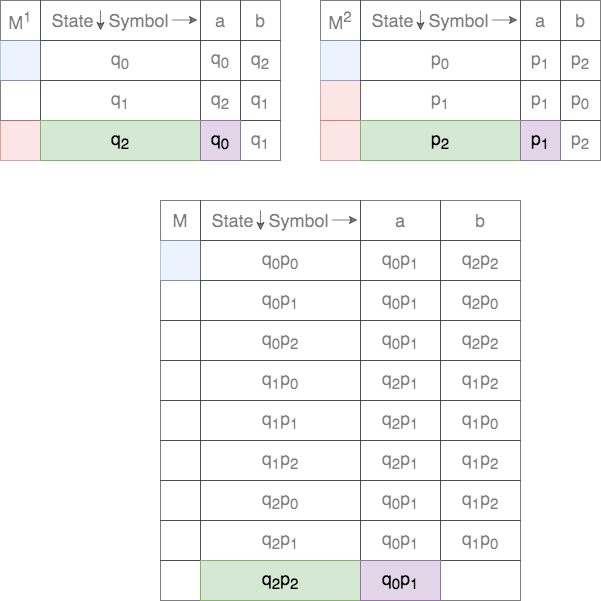
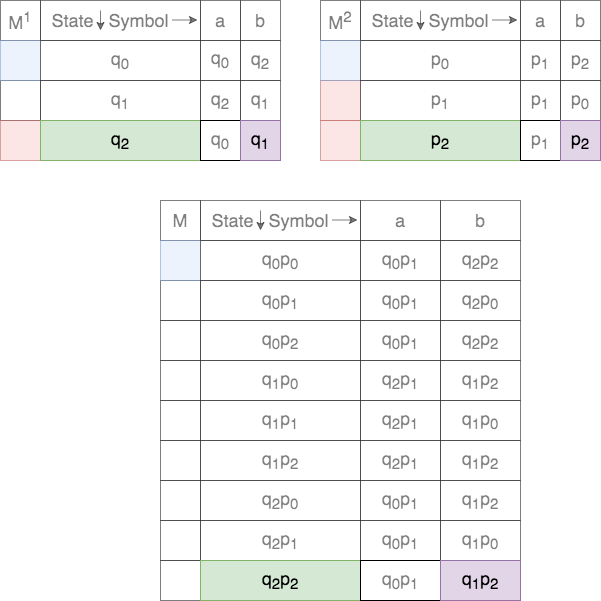
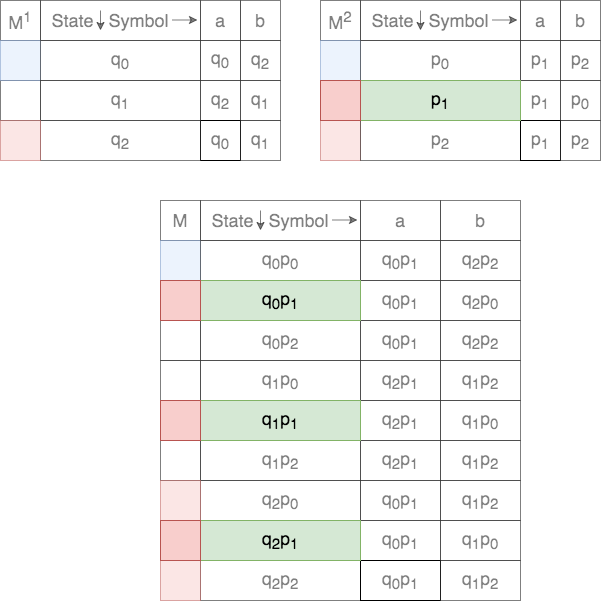
In case of union, the set of final states, ![]() , is defined as
, is defined as
Thus, any state that contains one element as final in either of the DFAs will be final.
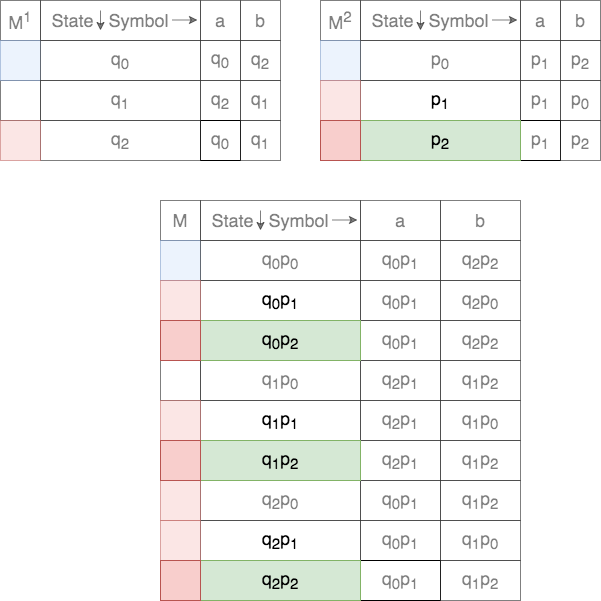
In case of intersection, the set of final states, ![]() , is defined as
, is defined as
Thus, any state that contains both the elements as final in each of the DFAs will be final.