A Hidden Markov Model is in essence a finite state machine. The states of the machine output an observable event with some probability. The states themselves are hidden and transition to each other with some probability.
Vocabulary
A vocabulary is a set of all possible observations. For example, here is a sequence of ![]() observations.
observations.
Observations can repeat and need not output every element in the Vocabulary
Observations
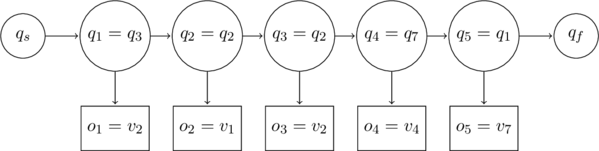
A sequence of ![]() observations. Each observation is output by a state. For the above example,
observations. Each observation is output by a state. For the above example, ![]() and
and
Length
A Hidden Markov Model is a sequence of ![]() observations and
observations and ![]() states. The
states. The ![]() extra states are the start and final states.
extra states are the start and final states.
Set of States
![]() is a set of
is a set of ![]() possible states. Special states,
possible states. Special states, ![]() and
and ![]() , denote the start and final states respectively.
, denote the start and final states respectively.
Hidden States
A Hidden Markov Model will start with ![]() , followed by
, followed by ![]() states and end with
states and end with ![]() . Here is a possible sequence of
. Here is a possible sequence of ![]() hidden states for the above example observations
hidden states for the above example observations
States can repeat and need not include every element in the Set of States
Indexing
A state/observation in the sequence of states/observations is indexed by ![]() . Thus,
. Thus,
Observation ![]() will be output by state
will be output by state ![]() . This state can be any state from the set
. This state can be any state from the set ![]() . A state in the set of states is indexed by
. A state in the set of states is indexed by ![]() or
or ![]() .,
.,
When the ![]() state in the sequence of states is state
state in the sequence of states is state ![]() , it is defined as follows
, it is defined as follows
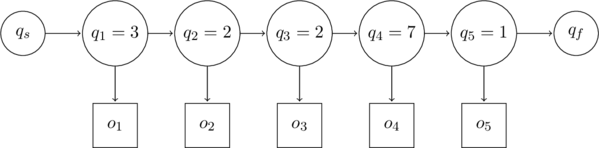
The above example can thus be redrawn as
Transition Probability Matrix
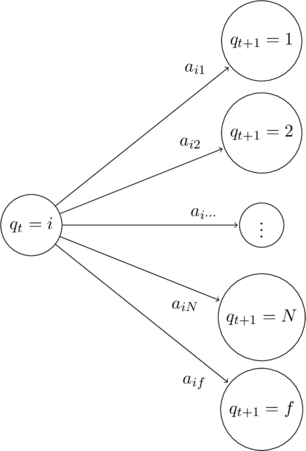
Transitions between the states are expressed as probabilities. ![]() denotes the probability of moving from state
denotes the probability of moving from state ![]() to state
to state ![]() .
.
A state has a transition probability to every other state in ![]() and the final state
and the final state ![]() .
.
By the law of total probability
The matrix can be defined as follows. Each row must add up to ![]() .
.
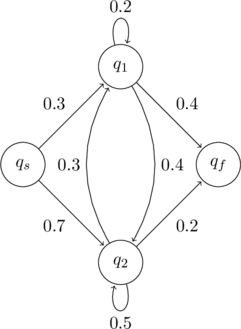
For simplicity, here is an example ![]() configuration
configuration
The Transition Probability Matrix for the above configuration will be
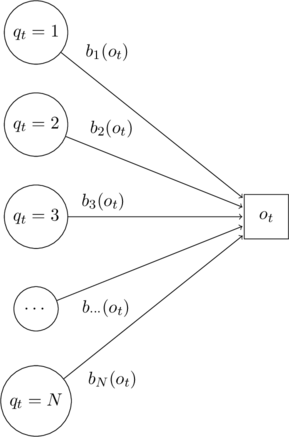
Observation Likelihood
The emission of an observation by a state is also expressed as a probability. ![]() is the probability of an observation
is the probability of an observation ![]() being generated from a state
being generated from a state ![]() . These are also called emission probabilities.
. These are also called emission probabilities.
Every state in ![]() has an emission probability for observation
has an emission probability for observation ![]() .
.
The matrix can be defined as follows
Extending the previous example
The Observation Likelihood Matrix for the above configuration will be
Hidden Markov Model
A Hidden Markov Model ![]() is thus defined by the above two matrices
is thus defined by the above two matrices ![]() and
and ![]() . This is written as
. This is written as
In addition, a first-order Hidden Markov Model also follows two simplifying assumptions.
Markov Assumption
The probability of a particular state depends only on the previous state
Output Independence
The probability of an output observation ![]() , depends only on the state that produced the observation
, depends only on the state that produced the observation ![]() and not on any other states or any other observations
and not on any other states or any other observations
Thank You
- Mark – for pointing out typos and errors
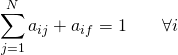
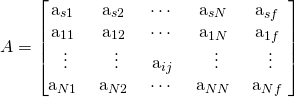
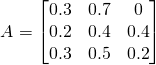
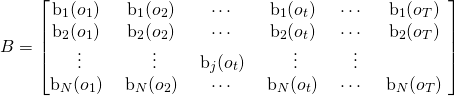
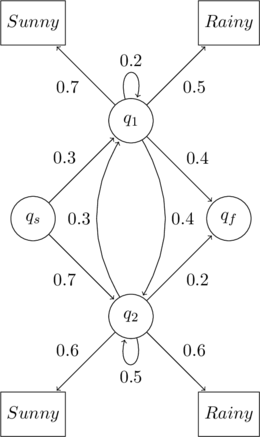
Thank you for the excellent write up! Very clearly explained. However, I believe the example state transition probability matrix (A) should have the 0.3 and 0.5 values in swapped positions on the bottom row (i.e. 0.3 0.5 0.2)
I have fixed the error you have pointed out. Thank you.