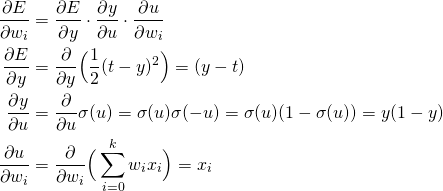This article explores the gradient descent algorithm for a single artificial neuron. The activation function is set to the logistic function.
Logistic Function
The logistic function is the most common kind of sigmoid function. It is defined as follows
Properties
The logistic function has two primary good properties
- The output
 is always between
is always between 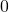 and
and 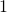 .
. - Unlike a unit step function,
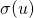 is smooth and differentiable, making the derivation of update equation very easy.
is smooth and differentiable, making the derivation of update equation very easy.
Single Artificial Neuron
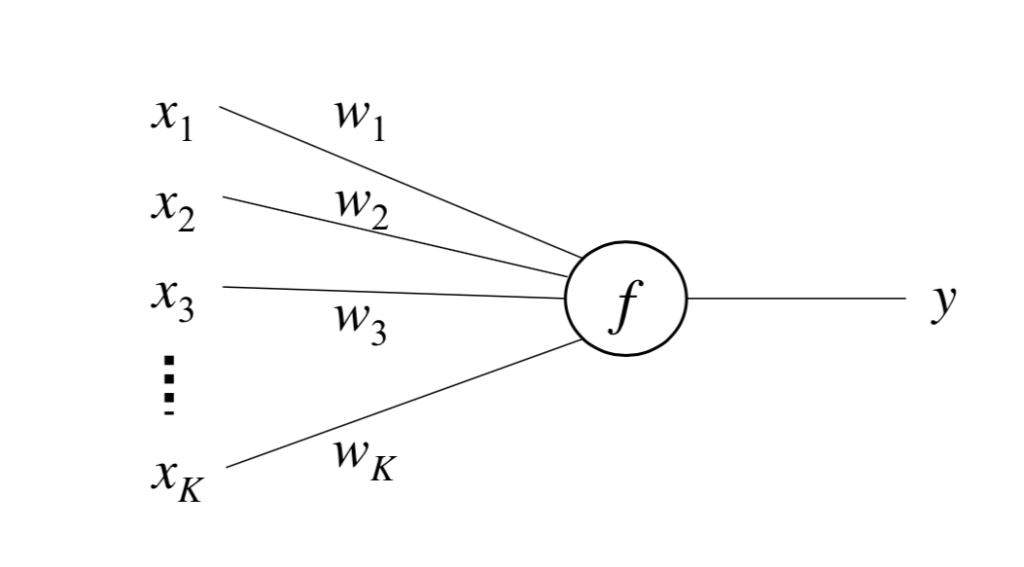
Notations
 are input values
are input values are weights
are weights is a scalar output
is a scalar output is the activation function (also called decision/transfer function)
is the activation function (also called decision/transfer function) is the label (gold standard)
is the label (gold standard) is is the learning rate (
is is the learning rate ( )
)
The unit works in the following way
where ![]() is a scalar number, which is the net input of the neuron.
is a scalar number, which is the net input of the neuron.
In vector notation
To include a bias term, simply add an input dimension (e.g., ![]() ) that is constant
) that is constant ![]() .
.
The error function (the training objective) is defined as
Use stochastic gradient descent as the learning algorithm of this model – take the derivative of ![]() with regard to
with regard to ![]()
Thus,
Once the derivative is computed, simply apply stochastic gradient descent for all samples