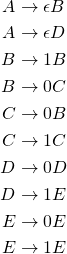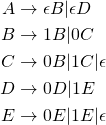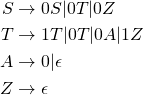A Context-Free Grammar (CFG) is a regular grammar if every rule is of the form
where ![]() and
and ![]() .
.
NFA to Regular Grammar
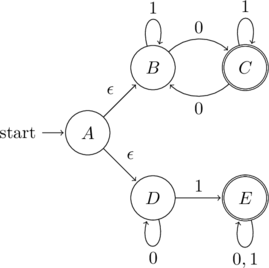
Consider the following NFA
The name of the states become the variables of the regular grammar. Each transition on an input symbol gets converted to a rule as shown below.
The final states will have the following additional rules
The start state of the NFA will be the start variable of the regular grammar (![]() ). Here is the final grammar in condensed form
). Here is the final grammar in condensed form
Regular Grammar to NFA
Consider the following regular grammar
To account for the ![]() rules, a new variable can be added as shown below
rules, a new variable can be added as shown below
Each rule defines the transition between states on that symbol. The variables that go to ![]() are marked as final. Here is an equivalent NFA.
are marked as final. Here is an equivalent NFA.