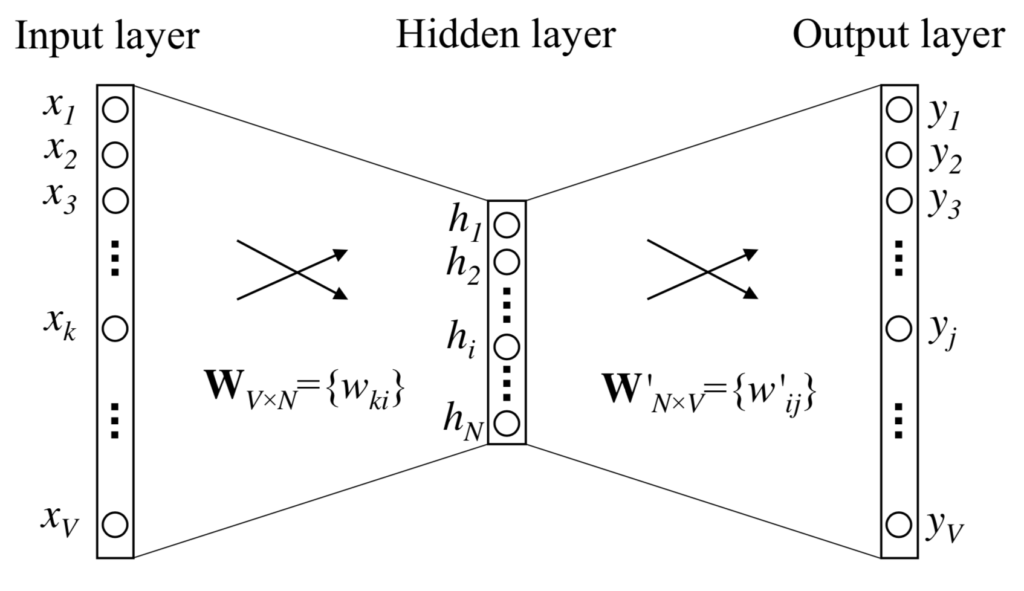
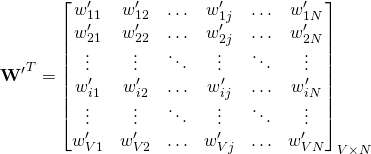The below figure shows a representation of Continuous Bag-of-Word Model with only one word in the context. There are three layers in total. The units on adjacent layers are fully connected.
Notations
- There are
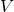 words in the vocabulary.
words in the vocabulary. - The input layer is of size
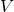 and indexed using
and indexed using 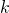 .
. - The output layer is of size
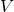 and indexed using
and indexed using 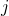 .
. - The hidden layer is of size
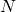 and indexed using
and indexed using 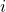 .
. 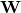 is the weight matrix connecting the input layer and the hidden layer.
is the weight matrix connecting the input layer and the hidden layer. 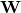 has dimensions
has dimensions  .
.- An individual element in the weight matrix
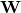 is denoted by
is denoted by  . Here.
. Here.  and
and  .
. 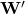 is the weight matrix connecting the hidden layer and the output layer.
is the weight matrix connecting the hidden layer and the output layer. 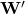 has dimensions
has dimensions  .
.- An individual element in the weight matrix
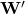 is denoted by
is denoted by 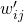 . Here.
. Here.  and
and 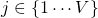 .
.
Input
The input is a one-hot encoded vector. This means that for a given input context word, only one out of ![]() units,
units, ![]() , will be
, will be ![]() , and all other units are
, and all other units are ![]() .
.
Consider an input word ![]() . Given a one-word context and the above one-hot encoding,
. Given a one-word context and the above one-hot encoding, ![]() and
and ![]() for
for ![]() .
.
Input-Hidden Weights
![]() is the weight matrix connecting the input layer and the hidden layer.
is the weight matrix connecting the input layer and the hidden layer. ![]() has dimensions
has dimensions ![]() .
.
An individual element in the weight matrix ![]() is denoted by
is denoted by ![]() . Here.
. Here. ![]() and
and ![]() . The transpose of the matrix is
. The transpose of the matrix is
From the network, the hidden layer is defined as follows
which is essentially copying the ![]() -th column of
-th column of ![]() (=
(= ![]() -th row of
-th row of ![]() ) to
) to ![]() . Thus, the
. Thus, the ![]() -th row of
-th row of ![]() is the
is the ![]() -dimension vector representation of the input word
-dimension vector representation of the input word ![]() . This is denoted by
. This is denoted by ![]()
Hidden-Output Weights
From the hidden layer to the output layer, there is a different weight matrix ![]() , which is an
, which is an ![]() matrix.
matrix.
An individual element in the weight matrix ![]() is denoted by
is denoted by ![]() . Here.
. Here. ![]() and
and ![]() . The transpose of the matrix is
. The transpose of the matrix is
From the network, the output layer is defined as follows
where ![]() is the
is the ![]() -th row of the matrix
-th row of the matrix ![]() (=
(= ![]() -th column of the matrix
-th column of the matrix ![]() ). Thus
). Thus
Each word in the vocabulary now has an associated score ![]() . Use softmax, a log-linear classification model, to obtain the posterior distribution of words, which is a multinomial distribution.
. Use softmax, a log-linear classification model, to obtain the posterior distribution of words, which is a multinomial distribution.
where ![]() is the output of the
is the output of the ![]() -th unit in the output layer.
-th unit in the output layer.
Note that ![]() and
and ![]() are two representations of the word
are two representations of the word ![]() .
. ![]() comes from rows of
comes from rows of ![]() , which is the input
, which is the input ![]() hidden weight matrix, and
hidden weight matrix, and ![]() comes from columns of
comes from columns of ![]() , which is the hidden
, which is the hidden ![]() output matrix.
output matrix.
Multi-Word Context
Multi-Word context is an extension of One-Word context. The input layer now has ![]() words instead of
words instead of ![]() . The below figure shows a representation of Continuous Bag-of-Word Model with multiple words in the context.
. The below figure shows a representation of Continuous Bag-of-Word Model with multiple words in the context.
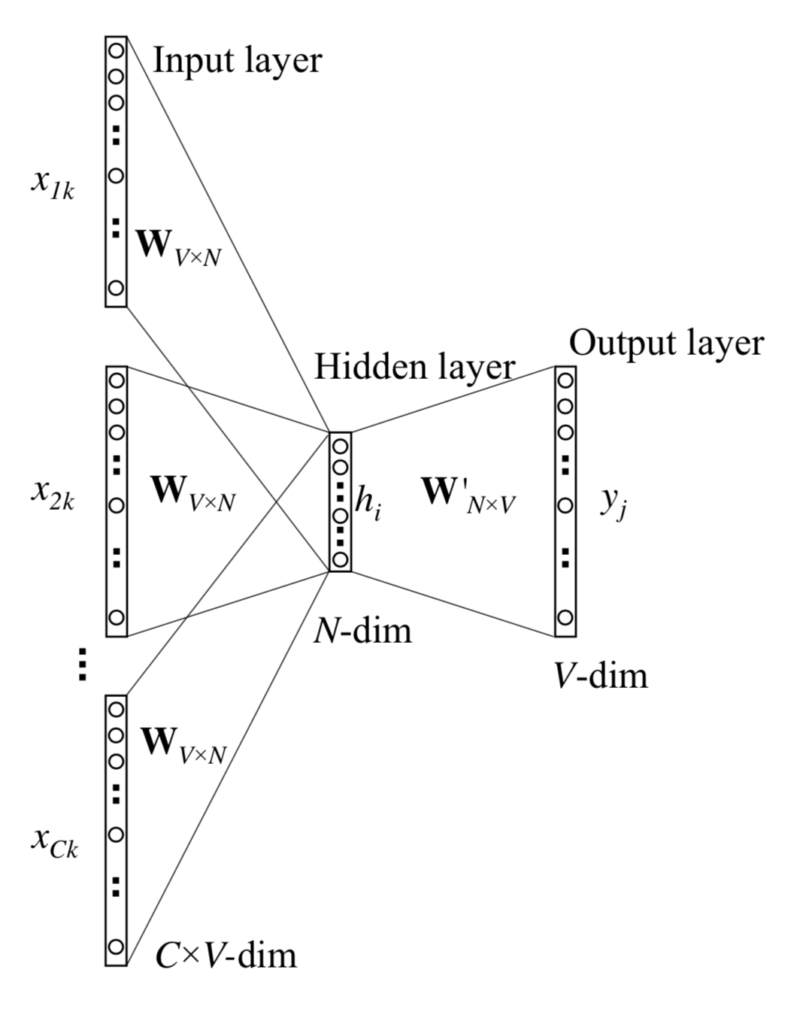
When computing the hidden layer output, instead of directly copying the input vector of the input context word, the CBOW model now takes the average of the vectors of the input context words, and use the product of the input ![]() hidden weight matrix and the average vector as the output.
hidden weight matrix and the average vector as the output.
where ![]() is the number of words in the context,
is the number of words in the context, ![]() are the words in the context, and
are the words in the context, and ![]() is the input vector of a word
is the input vector of a word ![]() .
.
Skip-Gram Model
The Skip-Gram model is the opposite of the Multi-Word CBOW model. The target word is now at the input layer, and the context words are in the output layer.
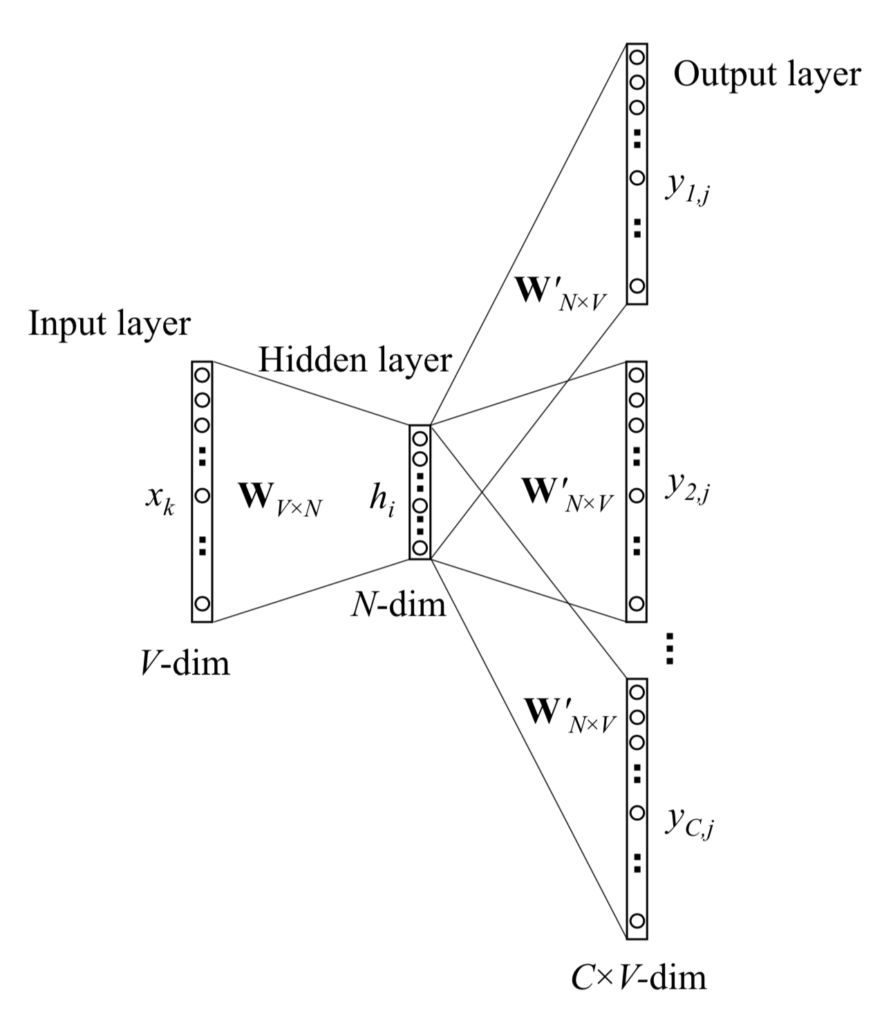
On the output layer, instead of outputing one multinomial distribution, there are ![]() multinomial distributions. Each output is computed using the same hidden
multinomial distributions. Each output is computed using the same hidden ![]() output matrix
output matrix
where ![]() is the
is the ![]() -th word on the
-th word on the ![]() -th panel of the output layer;
-th panel of the output layer; ![]() is the actual
is the actual ![]() -th word in the output context words;
-th word in the output context words; ![]() is the only input word;
is the only input word; ![]() is the output of the
is the output of the ![]() -th unit on the
-th unit on the ![]() -th panel of the output layer;
-th panel of the output layer; ![]() is the net input of the
is the net input of the ![]() -th unit on the
-th unit on the ![]() -th panel of the output layer. Because the output layer panels share the same weights,
-th panel of the output layer. Because the output layer panels share the same weights,
where ![]() is the output vector of the
is the output vector of the ![]() -th word in the vocabulary,
-th word in the vocabulary, ![]() , and also
, and also ![]() is taken from a column of the hidden
is taken from a column of the hidden ![]() output weight matrix,
output weight matrix, ![]() .
.