OpenCL - Kernel Space - The Beard Sage

NDRange

The index space supported by OpenCL is called an NDRange. An NDRange is an N-dimensional index space, where N is one, two or three. The NDRange is decomposed into work-groups forming blocks that cover the Index space. Each work-group consists of work-items which are conceptually similar to threads.

An NDRange is defined by two parameters

The global size in each dimension $G_x, G_y, G_z$
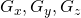
The local size in each dimension $S_x, S_y, S_z$

Work-item localId

Each work-item is assigned to a work-group and given a local ID to represent its position within the workgroup. A work-item’s local ID is an N-dimensional tuple with components in the range from zero to the size of the work-group in that dimension minus one. This is shown in the figure on the right.

$\begin{align*} 0 \leq s_x \leq S_x - 1 \\ 0 \leq s_y \leq S_y - 1 \\ \end{align*}$

Work-item globalId

A work-item can also be referenced directly using global indices. Each work-item’s global ID is an N-dimensional tuple. The global ID components are values in the range from 0, to the number of elements in that dimension minus one. This is shown in the figure on the left.

$\begin{align*} 0 \leq g_x \leq G_x - 1 \\ 0 \leq g_y \leq G_y - 1 \\ \end{align*}$

Work-group id

Work-groups are assigned IDs similarly. The number of work-groups in each dimension is not directly defined but is inferred from the local and global NDRanges provided. The number of work-groups in a dimension is the ceiling of the global size in that dimension divided by the local size in the same dimension.

$\begin{equation*} (W_x, W_y) = \Bigg(ceil\Bigg(\frac{G_x}{S_x}\Bigg), ceil\Bigg(\frac{G_y}{S_y}\Bigg)\Bigg) \end{equation*}$

A work-group’s ID is an N-dimensional tuple with components in the range 0 to the number of work-groups minus one.

$\begin{align*} 0 \leq w_x \leq W_x - 1 \\ 0 \leq w_y \leq W_y - 1 \\ \end{align*}$

The combination of a work-group ID and the local-ID within a workgroup uniquely defines a work-item. Each work-item is identifiable in two ways; in terms of a global index, and in terms of a work-group index plus a local index within a work group.

$\begin{equation*} (g_x, g_y) = (w_x * S_x + s_x, w_y * S_y + s_y) \end{equation*}$

$\begin{equation*} (w_x, w_y) = \Bigg(\frac{g_x - s_x}{S_x}, \frac{g_y - s_y}{S_y}\Bigg) \end{equation*}$

Global Dimensions

During kernel execution, each dimension is executed in parallel. A work-item (thread) is executed for every point in the global dimensions.

Global Dimensions	# Work Items
1024	1024
1920 * 1080	2M
256 * 256 * 256	16M

Local Dimensions

The global dimensions are broken down evenly into local work-groups. The host code can define the partitioning to work-groups, or leave it to the implementation.

Each work-group is logically executed together on one compute unit. Synchronization is only allowed between work-items in the same work-group.

Synchronization

A Work item is similar to a thread in terms of its control flow, and its memory model, distinguished from other executions within the collection by its global ID and local ID. Data sharing is possible between work items via local memory. Synchronization between work items happens via barriers and memory fences.

A Work group is a collection of related work-items that must map to a single compute unit. Work groups cannot synchronize with each other. OpenCL only supports global synchronization at the end of a kernel execution.

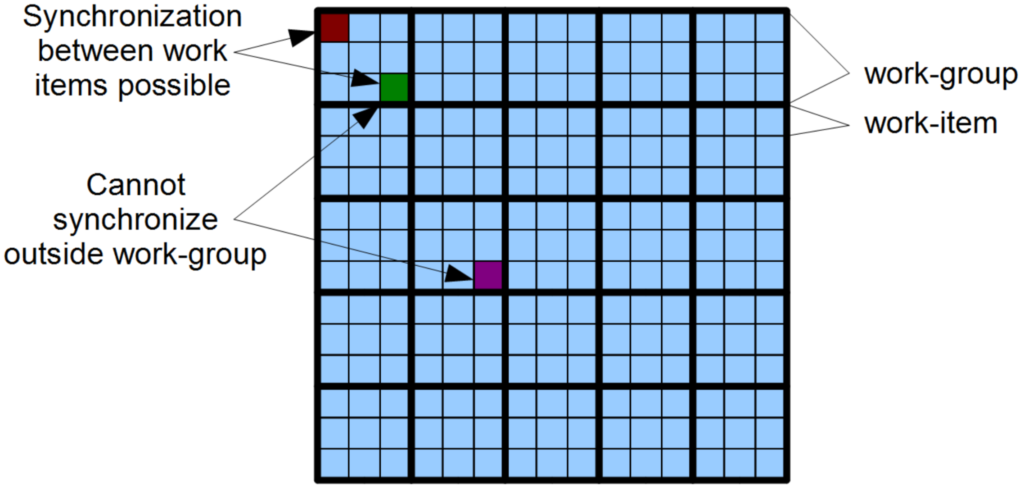
Device Utilization

An work-group runs in its entirety on one compute unit. Work-items within a work-group cannot be shared across compute units. If the size of a work-group does not match the hardware of the compute unit, it results in bad utilization.

For example consider a work-group that can hold $52$ threads. A compute unit has hardware to process $16$ threads at a time. The compute unit will work at full utilization during the first three cycles. During the last cycle only $52 - (16 * 3) = 4$ threads need to be run which leads in bad utilization.

If instead, the work-group was defined to hold $64$ threads, the compute unit will work at full utilization during all four cycles.

1 Comment → OpenCL – Kernel Space

Doug Gale March 23, 2023 at 5:19 am

This is the scenario that everyone focuses on. What I want to know, is what happens if you naively use loops in the kernel, and launch a 1 by 1 by 1 kernel. Is it so naive that it will laugh at you and just use one lane of the device, and do the whole thing completely sequentially? Or is it so smart that it will completely parallelize your loops right across compute units and synchronize it for you and everything?

It tries to auto-vectorize across at least one compute unit, right? The really obvious to optimize loops, I mean. Even if you are oblivious about work items? I’ve always wondered. It’s hard to measure – you’d have to do a naive-loops-you-hope-autovectorize implementation, then a smarty pants perfect-dimensions implementation, and compare them.

Reply ↓