Consider the following language definition
This language is not regular. This article explores a step by step approach to prove this by contradicting the Pumping Lemma for Regular languages.
Assumption
Suppose to the contrary ![]() is regular and
is regular and ![]() be its pumping length. Let
be its pumping length. Let ![]() and
and ![]() denote the number of
denote the number of ![]() and
and ![]() substrings in
substrings in ![]() respectively.
respectively.
Choosing a string
A string ![]() has to be chosen such that it satisfies the following two conditions
has to be chosen such that it satisfies the following two conditions
Consider the string ![]() .
.

Stating the Pumping Lemma
According to the Pumping Lemma for Regular languages, ![]() can be written as
can be written as ![]() , satisfying the following conditions
, satisfying the following conditions
Case 1: 
As ![]() ,
, ![]() will be composed entirely of ones. Without loss of generality
will be composed entirely of ones. Without loss of generality

Case 2: 
As ![]() ,
, ![]() must contain at least one
must contain at least one ![]() . Without loss of generality
. Without loss of generality

Case 3: 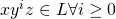
For ![]() to hold true
to hold true
This will hold true ![]() , if
, if ![]() . But according to Case 2,
. But according to Case 2, ![]() . This is a contradiction and all possible cases of expressing
. This is a contradiction and all possible cases of expressing ![]() have been considered.
have been considered.
Contradiction
The Pumping Lemma does not hold true. This means the assumption that ![]() is Regular was wrong. Thus,
is Regular was wrong. Thus, ![]() is not Regular.
is not Regular.




Pingback: Visualizing the Pumping Lemma for Regular Languages - TheBeardSage