All finite languages are regular. However, languages which accept infinite strings may or may not be regular. The pumping lemma describes a property of all regular languages. The intuition behind the lemma is that a sufficiently long string will have a middle section that can be pumped – repeated any number of times.
The pumping lemma holds true for all strings in a language that is regular. If the lemma does not hold true for some string that is in the language, then the language is not regular. Note that, the pumping lemma cannot be used to prove whether a language is regular. To prove a language is regular, one must define an NFA/DFA or produce a regular expression.
Formal Definition
Let ![]() be a regular language. There exists an integer
be a regular language. There exists an integer ![]() (called the pumping length), such that for every string
(called the pumping length), such that for every string ![]() in
in ![]() of length at least
of length at least ![]() ,
, ![]() can be written as
can be written as ![]() , satisfying the following conditions
, satisfying the following conditions
In essence, a string can be broken down into three parts – ![]() . The middle substring
. The middle substring ![]() can be pumped up indefinitely and yet the string remains in the language.
can be pumped up indefinitely and yet the string remains in the language.
Visualizing the Substrings
Consider the following string of length greater than ![]() . Each individual symbol is shown as a square block.
. Each individual symbol is shown as a square block.

This condition defines the span of the ![]() region. The remaining span makes up
region. The remaining span makes up ![]() . Notice that
. Notice that ![]() need not take up all
need not take up all ![]() symbols. However,
symbols. However, ![]() must start from the start of the string. The two spans for
must start from the start of the string. The two spans for ![]() and
and ![]() are shown in different colors below. Notice that for any possible split of
are shown in different colors below. Notice that for any possible split of ![]() and
and ![]() the pumping lemma holds true.
the pumping lemma holds true.

This condition defines the span of the ![]() region with the
region with the ![]() substring. For one of the above
substring. For one of the above ![]() and
and ![]() splits, all possible
splits, all possible ![]() and
and ![]() substrings are shown below.
substrings are shown below.

The last case is when ![]() is the empty string,
is the empty string, ![]() , and
, and ![]() takes up all the symbols in
takes up all the symbols in ![]() . Notice that for any possible split of
. Notice that for any possible split of ![]() and
and ![]() the pumping lemma holds true.
the pumping lemma holds true.
Consider all possible splits of ![]() into
into ![]() ,
, ![]() and
and ![]() by following the above constraints. No matter how
by following the above constraints. No matter how ![]() ,
, ![]() and
and ![]() are chosen, while pumping the
are chosen, while pumping the ![]() part of the string, the string remains in the language.
part of the string, the string remains in the language.
Using the Pumping Lemma to prove a Language is not Regular
Here is a general blueprint to use the Pumping Lemma to prove a Language is not Regular. An example problem is solved here.
Choosing a string 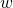
- Pick a string
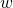 that belongs to the language.
that belongs to the language. 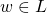
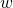 must be expressed in terms of
must be expressed in terms of  .
.- The length of
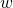 should be at least
should be at least  .
. 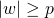
Contradicting the Pumping Lemma
- Consider all possible splits of
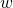 into
into 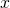 ,
,  and
and  , such that
, such that  .
. - Consider all possible splits of
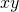 into
into 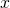 and
and  , such that
, such that  .
. - For all these cases, prove that, upon pumping, the string
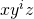 goes out of the language for some
goes out of the language for some 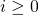 .
.
Since, all the conditions of the Pumping Lemma are not satisfied, the Language is not Regular.

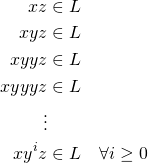
Pingback: Proving a Language is not Regular using the Pumping Lemma - TheBeardSage
Pingback: Proving a Language is not Regular using Closure Properties - TheBeardSage