Short Primer on Probability

Fundamentals

A random variable is denoted in capital, $V_i$ and the values it can take is denoted in small $v_i$ .

Consider a collection of $k$ random variables $(V_1, V_2, \cdots, V_k)$ . Random variables can be thought of as features of a particular domain of interest.

For example, the result of a coin toss can be represented using a single random variable, $C$ . This variable can take either of the categorical values $H$ or $T$ . If the same coin is tossed $k$ times, this can be represented using $k$ variables $(C_1, C_2, \cdots C_k)$ . Each of these values can be either $H$ or $T$ .

$\begin{equation*} C_i \in \{H, T\} \end{equation*}$

Joint Probability

An expression of the form $p(V_1, V_2, \cdots , V_k)$ is called a joint probability function over the variables $V_1, V_2, \cdots , V_k$ . The joint probability is defined when the values of $(V_1, V_2, \cdots , V_k)$ are $(v_1, v_2, \cdots, v_k)$ respectively. This is denoted by the expression

$\begin{equation*} p(V_1 = v_1, V_2 = v_2, \cdots , V_k = v_k) \end{equation*}$

This is sometimes abbreviated as $p(v_1, v_2, \cdots , v_k)$ .

For a fair coin toss, $p(H) = p(T) = 1/2$ . If a fair coin is tossed five times, $p(H,T,T,H,T) = 1/32$ .

The joint probability function satisfies

$\begin{equation*} 0 \leq p(V_1, V_2, \cdots , V_k) \leq 1 \end{equation*}$

$\begin{equation*} \sum p(V_1, V_2, \cdots , V_K) = 1 \end{equation*}$

Marginal Probability

The marginal probability of one of the random variables can be computed if the values of all of the joint probabilities for a set of random variables are known.

For example, the marginal probability $p(B=b)$ is defined to be the sum of all those joint probabilities for which $B=b$

$\begin{align*} p(B=b) & = \sum_{B=b}p(B,M,L,G) \\ p(B=b,M=m) & = \sum_{B=b,M=m}p(B,M,L,G) \\ \end{align*}$

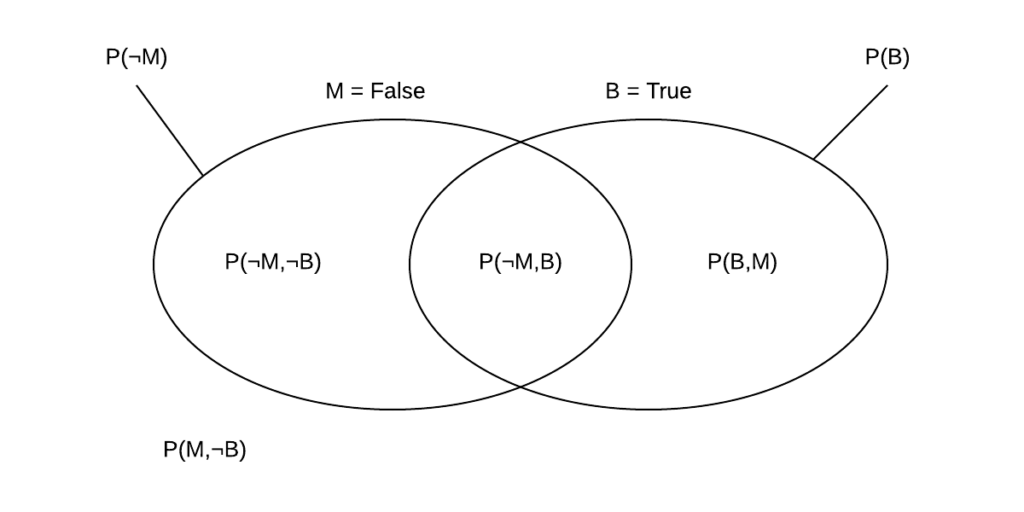
When dealing with propositional variables (True/False) $P(B=$ True $, M=$ False $)$ is denoted as $P(B, \neg M)$ .

Conditional Probabilities

The conditional probability of $V_i$ given $V_j$ is denoted by $P(V_i|V_j)$ .

$\begin{equation*} P(V_i|V_j) = \frac{P(V_i,V_j)}{P(V_j)} \end{equation*}$

where $P(V_i,V_j)$ is the joint probability of $V_i$ and $V_j$ and $P(V_j)$ is the marginal probability of $V_j$ . Thus

$\begin{equation*} P(V_i,V_j) = P(V_i|V_j){P(V_j)} \end{equation*}$

Joint conditional probabilities of several variables conditioned on several other variables is expressed as

$\begin{equation*} P(\neg G, B|\neg M, L) = \frac{P(\neg G, B, \neg M, L)}{P(\neg M, L)} \end{equation*}$

Venn diagram clearly illustrating conditional probability. Calculating marginal probability from joint probabilities is obvious. $P(B) = P(B,M) + P(B,\neg M)$ .

Venn diagram clearly illustrating conditional probability. Calculating marginal probability from joint probabilities is obvious. $P(B) = P(B,M) + P(B,\neg M)$ .

A joint probability can be expressed in terms of a chain of conditional probabilities.

$\begin{equation*} P(B,L,G,M) = P(B|L,G,M)P(L|G,M)P(G|M) \end{equation*}$

The general form of this chain rule is

$\begin{equation*} P(V_1, V_2, \cdots ,V_k) = \prod_{i=1}^k P(V_i|V_{i-1}, \cdots , V_1) \end{equation*}$

Bayes Rule

Different possible orders give different expressions but they all have the same value for the same set of variable values. Since the order of variables is not important

$\begin{equation*} P(V_i, V_j) = P(V_i|V_j)P(V_j) = P(V_j|V_i)P(V_i) = P(V_j,V_i) \end{equation*}$

Which gives Bayes’ Rule

$\begin{equation*} P(V_i| V_j) = \frac{P(V_j|V_i)P(V_i)}{P(V_j)} \end{equation*}$

Probabilistic Inference

In set notation $\mathcal{V} = {V_1, \cdots , V_k}$ , $P(\mathcal{V}) = P({V_1, \cdots , V_k})$ , The variables $V_1, \cdots, V_k$ having the values $v1, \cdots , v_k$ respectively is denoted by $\mathcal{V} = \bm{v}$ , where $\mathcal{V}$ and $\bm{v}$ are ordered lists.

For a set $\mathcal{V}$ , the variables in a subset $\mathcal{E} = \bm{e}$ of $\mathcal{V}$ are given as evidence.

$\begin{equation*} P({V}_i=True|\mathcal{E}=\bm{e}) = \frac{P({V}_i=True,\mathcal{E}=\bm{e})}{P(\mathcal{E}=\bm{e})} \end{equation*}$

$\begin{equation*} P({V}_i=True,\mathcal{E}=\bm{e}) = \sum_{{V}_i=True,\mathcal{E}=\bm{e}}P(V_1, \cdots , V_k) \end{equation*}$

For example, consider $\mathcal{V} = (V_1, V_2, V_3) = (P, Q, R)$ . The evidence $\mathcal{E}$ is $R$ being false. In other words $\mathcal{E} = e$ equates to $\neg R$ .

$\begin{equation*} P(Q|\neg R) = \frac{P(Q, \neg R)}{P(\neg R)} = \frac{\sum_{Q, \neg R} P(P, Q, R)}{P(\neg R)} = \frac{P(P,Q, \neg R) + P(\neg P,Q, \neg R)}{P(\neg R)} \end{equation*}$

$\begin{equation*} P(\neg Q|\neg R) = \frac{P(\neg Q, \neg R)}{P(\neg R)} = \frac{\sum_{\neg Q, \neg R} P(P, Q, R)}{P(\neg R)} = \frac{P(P,\neg Q, \neg R) + P(\neg P,\neg Q, \neg R)}{P(\neg R)} \end{equation*}$

$\begin{equation*} P(Q|\neg R) + P(\neg Q|\neg R) = 1 \end{equation*}$

Thus $P(\neg R)$ need not be computed.

Conditional Independence

A variable $V$ is conditionally independent of a set of variables $\mathcal{V}_i$ given a set $\mathcal{V}_j$ if

(1)

$\mathcal{V}_i$ tells nothing more about $\mathcal{V}$ than is already known by knowing $\mathcal{V}_j$ .

(2)

Saying that $V_i$ is conditionally independent of $V_j$ given $\mathcal{V}$ also means that $V_j$ is conditionally independent of $V_i$ given $\mathcal{V}$ . The same result also applies to sets $\mathcal{V}_i$ and $\mathcal{V}_j$ .

As a generalization of pairwise independence, the variables $V_1, \cdots , V_k$ are mutually conditionally independent, given a set $\mathcal{V}$ if each of the variables is conditionally independent of all of the others given $\mathcal{V}$ .

(3)

When $\mathcal{V}$ is empty

$\begin{equation*} P(V_1, V_2, \cdots , V_k) = P(V_1)\cdot P(V_2)\cdot \cdot \cdot P(V_k) \end{equation*}$

This implies that the variables are unconditionally independent.

Thank You

Mark – for pointing out typos and errors

2 Comments → Short Primer on Probability

Mark March 4, 2020 at 12:54 am

Another great article! Nice, clear explanations.

I do have some suggestions for improvement though:

It seems there is an error in the Bayes Rule section. It should be P(V_i|V_j) = P(V_j|V_i)P(V_i)/P(V_j)

I would also recommend explaining how you introduced the P and not P random variables in the Probabilistic Inference section as it is not quite clear how that works out.

Finally, it seems your Latex implementation had trouble rendering for the fourth paragraph in the Conditional Independence section (\textbf{mutually conditionally independent}), right above equation (3).

Reply ↓
1. TheBeard March 4, 2020 at 4:11 am
  
  I have expanded the Probabilistic Inference section and fixed the errors you have pointed out. Thank you.
  
  Reply ↓

The Beard Sage