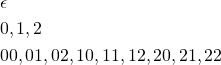The transition function of a Non-Deterministic Turing Machine (NDTM) is mapped as follows
Similar to an NFA, an NDTM has multiple choices to change states. If there is some path that leads to ![]() , it leads to an accepting computation.
, it leads to an accepting computation.
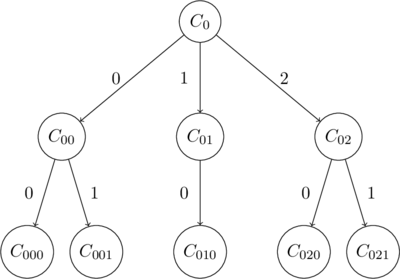
Computation Tree
The computation process of an NDTM can be visualized as a tree. Each node of the tree is a configuration. The subscripts denote the path to reach that node from the root. ![]() is the initial configuration.
is the initial configuration.
Here is an example tree
Depth-First vs Breadth-First
A Depth-First search of the above tree can lead to an infinite search if a computation never halts on some branch.
However, a Breadth-First search will find an accepting computation at some finite depth. To carry out this search the tree needs an addressing mechanism.
Address
The transition function maps ![]() to a finite number of states. This number corresponds to the number of children at a given node. Let
to a finite number of states. This number corresponds to the number of children at a given node. Let ![]() be the maximum value of
be the maximum value of ![]() given any
given any ![]() and
and ![]() . In essence,
. In essence, ![]() is the maximum number of children for any node in the computation tree.
is the maximum number of children for any node in the computation tree.
In the above example ![]() . Using this information, construct
. Using this information, construct ![]() -bit addresses in non-decreasing order of length. This order emulates Breadth-First search.
-bit addresses in non-decreasing order of length. This order emulates Breadth-First search.
Each address corresponds to a path in the computation tree (if it exists). For example
Multi-tape Deterministic Turing Machine
Here is the high-level description of an equivalent Multi-tape Deterministic TM for a NDTM.
The Turing Machine will have three tapes – input, work and address.
The input tape is populated with the input string.
On the address tape, enumerate the members of ![]() in non-decreasing order of length.
in non-decreasing order of length.
- Copy input tape to the work tape.
- On the work and address tapes, position the tape-heads at the left.
- Carry out the computation by emulating the contents on the address tape. This is basically a Breadth-First computation of the tree.
- If the machine enters
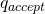 , accept and halt.
, accept and halt. - If the machine enters
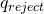 , increment the address and repeat from step 1.
, increment the address and repeat from step 1. - If the entire address is read (and the machine is not in
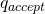 , increment the address and repeat from step 1.
, increment the address and repeat from step 1.