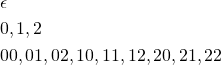Turing Machine Variant - Nondeterminism

The transition function of a Non-Deterministic Turing Machine (NDTM) is mapped as follows

$\begin{equation*} Q \setminus \{q_{accept}, q_{reject}\} \times \Gamma \rightarrow \mathcal{P}(Q \times \Gamma \times \{L, R\}) \end{equation*}$

Similar to an NFA, an NDTM has multiple choices to change states. If there is some path that leads to $q_{accept}$ , it leads to an accepting computation.

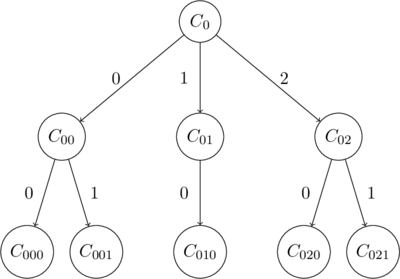
Computation Tree

The computation process of an NDTM can be visualized as a tree. Each node of the tree is a configuration. The subscripts denote the path to reach that node from the root. $C_0$ is the initial configuration.

Here is an example tree

Rendered by QuickLaTeX.com

Depth-First vs Breadth-First

A Depth-First search of the above tree can lead to an infinite search if a computation never halts on some branch.

However, a Breadth-First search will find an accepting computation at some finite depth. To carry out this search the tree needs an addressing mechanism.

Address

The transition function maps $\delta(q, x)$ to a finite number of states. This number corresponds to the number of children at a given node. Let $d$ be the maximum value of $\delta(q, x)$ given any $q$ and $x$ . In essence, $d$ is the maximum number of children for any node in the computation tree.

In the above example $d = 3$ . Using this information, construct $d$ -bit addresses in non-decreasing order of length. This order emulates Breadth-First search.

$\begin{align*} & \epsilon \\ & 0, 1, 2 \\ & 00, 01, 02, 10, 11, 12, 20, 21, 22 \\ \end{align*}$

Each address corresponds to a path in the computation tree (if it exists). For example

$\begin{equation*} 21 \implies C_0 \vdash C_{02} \vdash C_{021} \end{equation*}$

Multi-tape Deterministic Turing Machine

Here is the high-level description of an equivalent Multi-tape Deterministic TM for a NDTM.

The Turing Machine will have three tapes – input, work and address.

The input tape is populated with the input string.

On the address tape, enumerate the members of $\{1, \cdots, d\}^*$ in non-decreasing order of length.

Copy input tape to the work tape.
On the work and address tapes, position the tape-heads at the left.
Carry out the computation by emulating the contents on the address tape. This is basically a Breadth-First computation of the tree.
If the machine enters 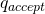$q_{accept}$ , accept and halt.
If the machine enters 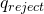$q_{reject}$ , increment the address and repeat from step 1.
If the entire address is read (and the machine is not in 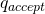$q_{accept}$ , increment the address and repeat from step 1.

The Beard Sage

Turing Machine Variant – Nondeterminism

Computation Tree

Depth-First vs Breadth-First

Address

Multi-tape Deterministic Turing Machine

Leave a Reply Cancel reply