Turing Machine Variant - Multiple Tapes

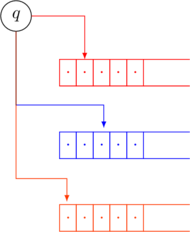
A multi-tape Turing Machine (TM) is a TM with access to a fixed finite number of tapes. A $k$ -tape TM has access to $k$ tapes.

Rendered by QuickLaTeX.com

Initial Configuration

The input string is placed on the first tape. All other tapes are blank. All tape heads point to the start of their respective tapes.

Rendered by QuickLaTeX.com

Transition Function

The transition function $\delta$ is mapped as follows

$\begin{equation*} Q \times \Gamma^k \rightarrow Q \times (\Gamma \times \{L, R, S\})^k \end{equation*}$

Based on the current state and the current-tape cell read by each of the $k$ tapes, the transition specifies the next state, what to write on each of the $k$ tapes and the direction to move the tape-head on each of the $k$ tapes.

The direction $S$ implies staying on the current cell.

Rendered by QuickLaTeX.com

$\begin{equation*} \delta(q, (x_1, y_2, z_3)) = (q, (X_1, R), (Y_2, L), (Z_3, S)) \end{equation*}$

Rendered by QuickLaTeX.com

Equivalence to Single Tape

Rendered by QuickLaTeX.com

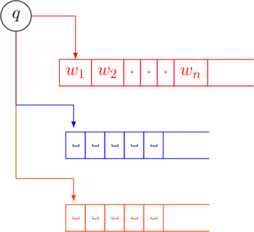
Any multi-tape Turing Machine computation can be carried out by an equivalent single-tape Turing Machine.

Rendered by QuickLaTeX.com

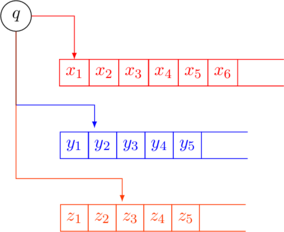
The single-tape TM has the tape contents of the individual tapes separated by a separator symbol ( $\#$ ). The tape-head of each individual tape is marked by the dotted equivalent of the symbol it points to.

To carry out one transition of a $k$ -tape TM on the single-tape

Scan right to the first dotted symbol. Remember this symbol in the current state.
Repeat step 1 to scan and remember 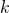$k$ symbols in the current state.
The current state and the 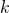$k$ symbols will have a finite number of possibilities.
Use the transition function to find the next configuration.
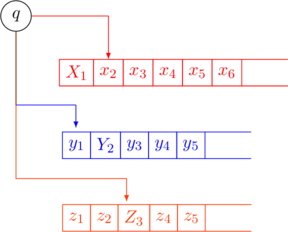
Bring tape-head back to the start.
Scan right to the first dotted symbol. Apply the configuration for the first tape. This involves writing a symbol, and moving the tape-head (reapplying the dot). If the dotted symbol is one cell to the left of a separator, a new blank cell must be added to accommodate for a $R$ transition.
Repeat step 6 to scan and apply the configuration for each of the 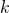$k$ tapes.

Remembering symbols

A Turing Machine can remember by using specific states. Say the tape alphabet is $\{0, 1\}$ and there are $3$ tapes. There can be a state $qp_{010}$ to remember that the current state is $q$ , the tape-heads point to $0$ on the first-tape, $1$ on the second-tape and $0$ on the third-tape. From this state it can make an appropriate transition by following the transition function.

Finite number of possibilities

To remember multiple symbols, a single-tape TM equivalent to a $k$ -tape TM (with $Q$ states) will need $|\Gamma|^k$ new states for each of the $Q$ states for a total of $|Q||\Gamma|^k$ states.

Adding a new blank cell

Adding a new blank cell involves shifting all the contents of the tape one cell to the right. This has to be done in a right-most first fashion.

Conclusion

A language $L$ is recognized by a single-tape TM if and only if $L$ is recognized by a $k$ -tape TM.

A language $L$ is decided by a single-tape TM if and only if $L$ is decided by a $k$ -tape TM.

The Beard Sage

Turing Machine Variant – Multiple Tapes

Initial Configuration

Transition Function

Equivalence to Single Tape

Remembering symbols

Finite number of possibilities

Adding a new blank cell

Conclusion

Leave a Reply Cancel reply