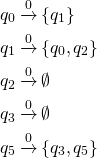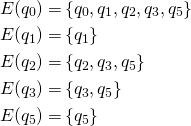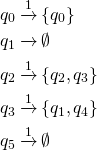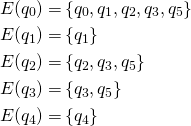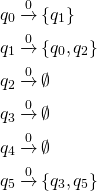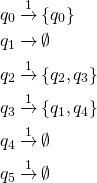Both deterministic and non-deterministic finite machines recognize the set of regular languages. This article explores a step by step approach to convert a NFA to a DFA that accepts the same language.
NFA
Consider the following NFA
| State | |||
|---|---|---|---|
This NFA can be converted into an equivalent DFA by following these steps
Compute  -close set
-close set
The ![]() -close set of a state is defined as the set of all states that can be reached by following
-close set of a state is defined as the set of all states that can be reached by following ![]() or more
or more ![]() transitions from that state. The
transitions from that state. The ![]() -close set of a state will always contain that state. The
-close set of a state will always contain that state. The ![]() -close set of all the states of the NFA are computed
-close set of all the states of the NFA are computed
| State | ||||
|---|---|---|---|---|
Start state of DFA
The start state of DFA will be the epsilon closure of start state of NFA. In this case
| State | 0 | 1 |
|---|---|---|
Transition on 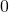 followed by
followed by  -close
-close
Track the transition for each state in the above set and combine the result.
Thus,
Take the ![]() -close of this set
-close of this set
Thus, the final state is given by
| State | 0 | 1 |
|---|---|---|
Transition on 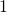 followed by
followed by  -close
-close
Track the transition for each state in the above set and combine the result.
Thus,
Take the ![]() -close of this set
-close of this set
Thus, the final state is given by
| State | 0 | 1 |
|---|---|---|
The above process has to be repeated until no more new states are being added and all transitions are accounted for. In this case there is a new state.
Transition on 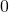 followed by
followed by  -close
-close
Track the transition for each state in the above set and combine the result.
Thus,
Take the ![]() -close of this set
-close of this set
Thus, the final state is given by
| State | 0 | 1 |
|---|---|---|
Transition on 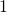 followed by
followed by  -close
-close
Track the transition for each state in the above set and combine the result.
Thus,
Take the ![]() -close of this set
-close of this set
Thus, the final state is given by
| State | 0 | 1 |
|---|---|---|
No new states are added an all transitions are accounted for.
Final states
If a state in the DFA has any occurrence of a final state in the original NFA, it is marked final. In the above case, ![]() and
and ![]() are final in the original NFA. This makes both the states in the DFA final.
are final in the original NFA. This makes both the states in the DFA final.
| State | 0 | 1 |
|---|---|---|
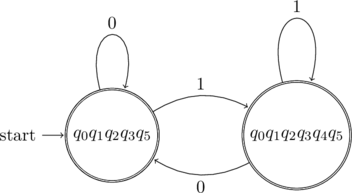
State Diagram
Here is an equivalent transition state diagram