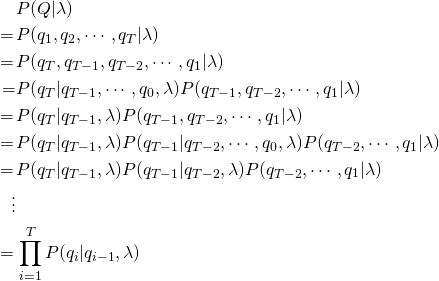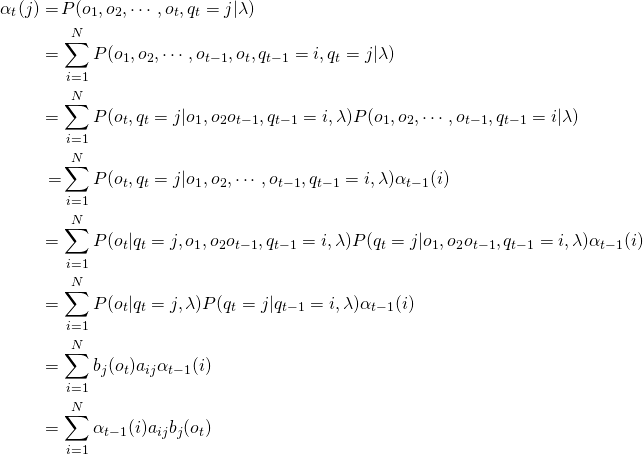Computing Likelihood
Given an Hidden Markov Model defined by ![]() and an observation sequence
and an observation sequence ![]() , determine the likelihood that the observation sequence was generated by this model,
, determine the likelihood that the observation sequence was generated by this model, ![]() .
.
For a particular hidden state sequence ![]() and an observation sequence
and an observation sequence ![]() , the likelihood of the observation sequence is defined as
, the likelihood of the observation sequence is defined as
The likelihood of the state sequence is defined as follows. The start state is excluded for now and added at the end.
where ![]() is the same as the start state
is the same as the start state ![]() .
.
Combining the two results above
The total probability of the observations can be computed by summing over all possible hidden state sequences
Time Complexity
A sequence ![]() can have
can have ![]() combinations.
combinations.
| Term | Time Complexity |
Thus the total time complexity will be ![]() .
.
Forward Algorithm
The forward algorithm (a kind of dynamic programming algorithm) is an efficient algorithm, that uses a table to store intermediate values as it builds up the probability of the observation sequence. The forward algorithm computes the observation probability by summing over the probabilities of all possible hidden state paths that could generate the observation sequence, but it does so efficiently by implicitly folding each of these paths into a single forward trellis.
![]() represents the probability of being in state
represents the probability of being in state ![]() after seeing the first
after seeing the first ![]() observations, given the Hidden Markov Model
observations, given the Hidden Markov Model ![]() .
. ![]() is computed by summing over the probabilities of every path that could lead to this state.
is computed by summing over the probabilities of every path that could lead to this state.
where ![]() is the previous forward path probability from the previous time step.
is the previous forward path probability from the previous time step.
Visualization
Visualizing the computation of a single element ![]() in the trellis by summing all the previous values
in the trellis by summing all the previous values ![]() , weighted by their transition probabilities
, weighted by their transition probabilities ![]() , and multiplying by the observation probability
, and multiplying by the observation probability ![]() . Hidden states are in circles, observations in squares. Shaded nodes are included in the probability computation for
. Hidden states are in circles, observations in squares. Shaded nodes are included in the probability computation for ![]() .
.
Initialization
Recursion
Termination
Time Complexity
Initialization step runs in ![]() . Recursion step is run
. Recursion step is run ![]() times and the summation is over
times and the summation is over ![]() . Thus, the recursion step runs in
. Thus, the recursion step runs in ![]() . Termination step runs in
. Termination step runs in ![]() . The forward algorithm thus reduces the time complexity to
. The forward algorithm thus reduces the time complexity to ![]() .
.