A Turing Machine can end up in one of three possibilities
- Accept and halt by ending up in
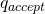 .
. - Reject and halt by ending up in
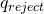 .
. - Run forever.
Turing Recognizable
The language recognized by a Turing Machine is the set of strings that the machine accepts.
A language is Turing recognizable if it is recognized by some Turing Machine. Thus, if a string belongs to a a language that is Turing recognizable, there exists some Turing Machine which will accept that string. However, strings that do not belong to the language may run forever.
Turing Decidable
A Turing Machine is a decider if it halts on every input.
A language is Turing decidable if it is recognized by a Turing Machine decider. Thus, in addition to the Turing Machine accepting all strings that belong to the language, it should reject all strings that do not belong to the language. The machine halts on every input.
It is easy to see that every Turing Decidable language is Turing Recognizable.
Turing Enumerable
A Turing Machine (with an additional output tape) is an enumerator for a language if when started on an empty input, it writes all strings that belong to the language on the output tape. For the sake of clarity, each string is separated by a distinct symbol.
A TM enumerator ensures two things
- Only strings that belong to the language appear on the output tape
- If a string belongs to the language, it will be written on the ouput tape after some finite amount of time.
While enumerating, the strings can appear multiple times or/and out-of-order.
A language is Turing enumerable if some Turing Machine enumerates it.
Enumerable implies Recognizable
Say the language ![]() is Turing Enumerable. Let the machine
is Turing Enumerable. Let the machine ![]() be the enumerator for it.
be the enumerator for it.
To recognize ![]()
- On input
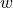 , run
, run 
- When
 outputs a string, say
outputs a string, say 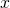 , check whether
, check whether  .
. - If yes, accept.
If ![]() , after a finite amount of time it will be accepted. If
, after a finite amount of time it will be accepted. If ![]() , the machine may run forever.
, the machine may run forever.
Recognizable implies Enumerable
Say the language ![]() is Turing Recognizable. Let the machine
is Turing Recognizable. Let the machine ![]() be the recognizer for it.
be the recognizer for it.
To enumerate ![]()
- On empty input
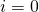
- Repeat
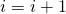
- Generate first
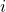 strings (in some order) from
strings (in some order) from 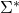 . Let these be
. Let these be  .
. - For each
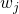
- Run
 on
on 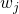 for at max
for at max 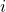 transitions
transitions - If
 accepts
accepts 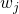 , print
, print 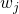 on the output tape
on the output tape
- Run
Each string ![]() is limited to
is limited to ![]() number of transitions on
number of transitions on ![]() . This ensures that the above algorithm never gets stuck.
. This ensures that the above algorithm never gets stuck. ![]() is incremented in each iteration. This gives the option to rerun
is incremented in each iteration. This gives the option to rerun ![]() on the same string for greater number of transitions.
on the same string for greater number of transitions.
Say ![]() accepts
accepts ![]() in
in ![]() transitions. Let
transitions. Let ![]() be the
be the ![]() string in order in
string in order in ![]() . Then, the enumerator is guaranteed to output the string in
. Then, the enumerator is guaranteed to output the string in ![]() iterations.
iterations.
Every string that is accepted gets printed on the output tape infinite number of times.