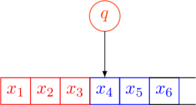
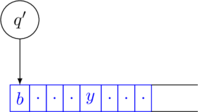
Snapshot as a String
A configuration of a Turing Machine is a snapshot of the current state of the machine. It is expressed as a string.
The string has three components
- the tape contents to the left of the tape-head
- the current state
- the tape contents to the right of the tape-head (including the current cell)
These components are shown in different colors below
The configuration of the above snapshot will be
Formal Definition
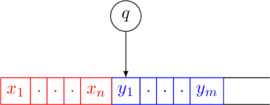
A configuration of a Turing Machine is a string ![]() where
where
- the tape contents are
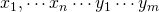 . This is followed by infinite blanks
. This is followed by infinite blanks  .
. - the tape-head is pointing at
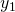
- the current state is

Note that after ![]() all the tape cells are
all the tape cells are ![]() . Thus there are infinite such configurations for a given snapshot.
. Thus there are infinite such configurations for a given snapshot.
A configuration can thus be written as ![]() where
where ![]() and
and ![]() are the tape-contents in the red and blue region respectively.
are the tape-contents in the red and blue region respectively.
It makes perfect sense for ![]() to be the empty string, but
to be the empty string, but ![]() should have at least one symbol (the cell the tape-head is pointing to).
should have at least one symbol (the cell the tape-head is pointing to).
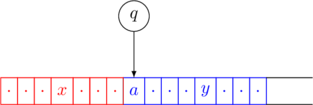
Right Transition
Suppose that the current configuration is ![]() where
where ![]() ,
, ![]() and
and ![]() .
.
Consider the following transition ![]()
The configuration changes to ![]() .
.
This is denoted as
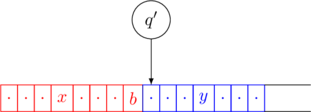
Left Transition
Suppose that the current configuration is ![]() where
where ![]() ,
, ![]() and
and ![]() .
.
Consider the following transition ![]()
The configuration changes to ![]() .
.
This is denoted as
![]() ensures that the tape-head is not pointing at the left end of the tape. If the configuration is
ensures that the tape-head is not pointing at the left end of the tape. If the configuration is ![]() , the same transition will not move the tape-head.
, the same transition will not move the tape-head.
Initial Configuration
On input string ![]() when the configuration is
when the configuration is
it is called a starting or initial configuration.
Accepting Configuration
A configuration of the form
is called an accepting configuration.
Rejecting Configuration
A configuration of the form
is called an rejecting configuration.
Computation
A computation on a Turing Machine is a series of configurations ![]() such that
such that
and ![]() is the initial configuration.
is the initial configuration.
If in addition ![]() is accepting then the string is accepted by the machine – accepting computation
is accepting then the string is accepted by the machine – accepting computation
If instead ![]() is rejecting then the string is rejected by the machine – rejecting computation
is rejecting then the string is rejected by the machine – rejecting computation
There can be computations where the string is neither accepted or rejected. The Turing Machine runs forever.
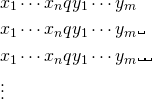


Pingback: Turing Machine Variant - Nondeterminism - TheBeardSage